Skip to contents

Extending the INTERGROWTH-21st Newborn Size Standards

Source: vignettes/articles/extending-ig-nbs.rmd
extending-ig-nbs.rmd

Setup 

#> Loading required package: survival

Rationale

Over the years, there have been many requests from users of the INTERGROWTH-21st Newborn Size Standards (including the Very Preterm standards) to extend their range from 168 to 300 days (24+0 to 42+6 weeks) gestational age (GA) to a wider span of 154 to 314 days (22+0 to 44+6 weeks) GA. We’ve decided to implement this in gigs as an entirely separate standard from the INTERGROWTH-21st Newborn Size standards, to make these extended versions of the standards available to all.

We want to note here that this process has been checked over by the former Lead Statistician for the INTERGROWTH-21st Project, Eric Ohuma, but is not endorsed officially by INTERGROWTH-21st. We want users to be aware that z-scores/centiles derived from these extended bounds must be used with caution - it is at the user’s discretion to ensure they are careful with these extended standards.

Approach

For the Very Preterm standards

For the INTERGROWTH-21st Very Preterm standards, extending the standards is easy. The Very Preterm standards use simple equations to model the mean and standard deviation at different gestational ages (GAs). Extending these standards is as simple as using gestational age values from 154 to 167 in these equations.

For the Newborn Size standards

The INTERGROWTH-21st Newborn Size standards are more difficult to extend as they are coefficient-based. For each gestational age from 231 days (33+0 weeks) to 300 days (42+6 weeks), there are corresponding mu/sigma/nu/tau values. These are used with gamlss.dist::pST3() to convert values to centiles in these standards, and with gamlss.dist::qST3() to convert centiles to values. Each coefficient represents a different aspect of the distribution of anthropometric measures at a given gestational age:

  • mu - The median of the distribution at a given GA.
  • sigma - The standard deviation of the distribution at a given GA.
  • nu - The skewness of the distribution at a given GA.
  • tau - The kurtosis of the distribution at a given GA.

To extend these standards out, we need to generate new coefficients for gestational ages from 301 to 314 days (43+0 to 44+6 weeks). We will do this with fractional polynomial regression in {mfp} package.

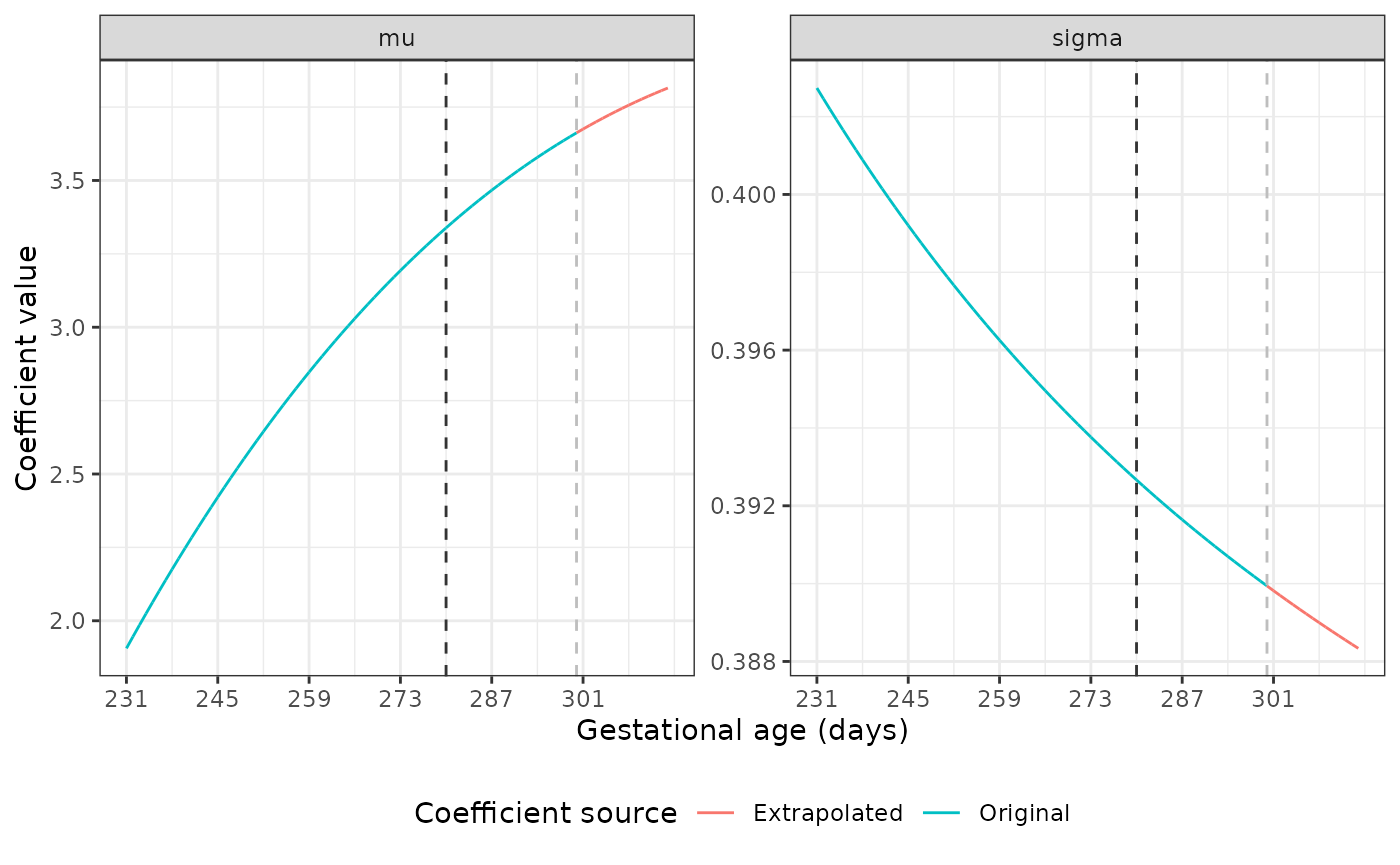
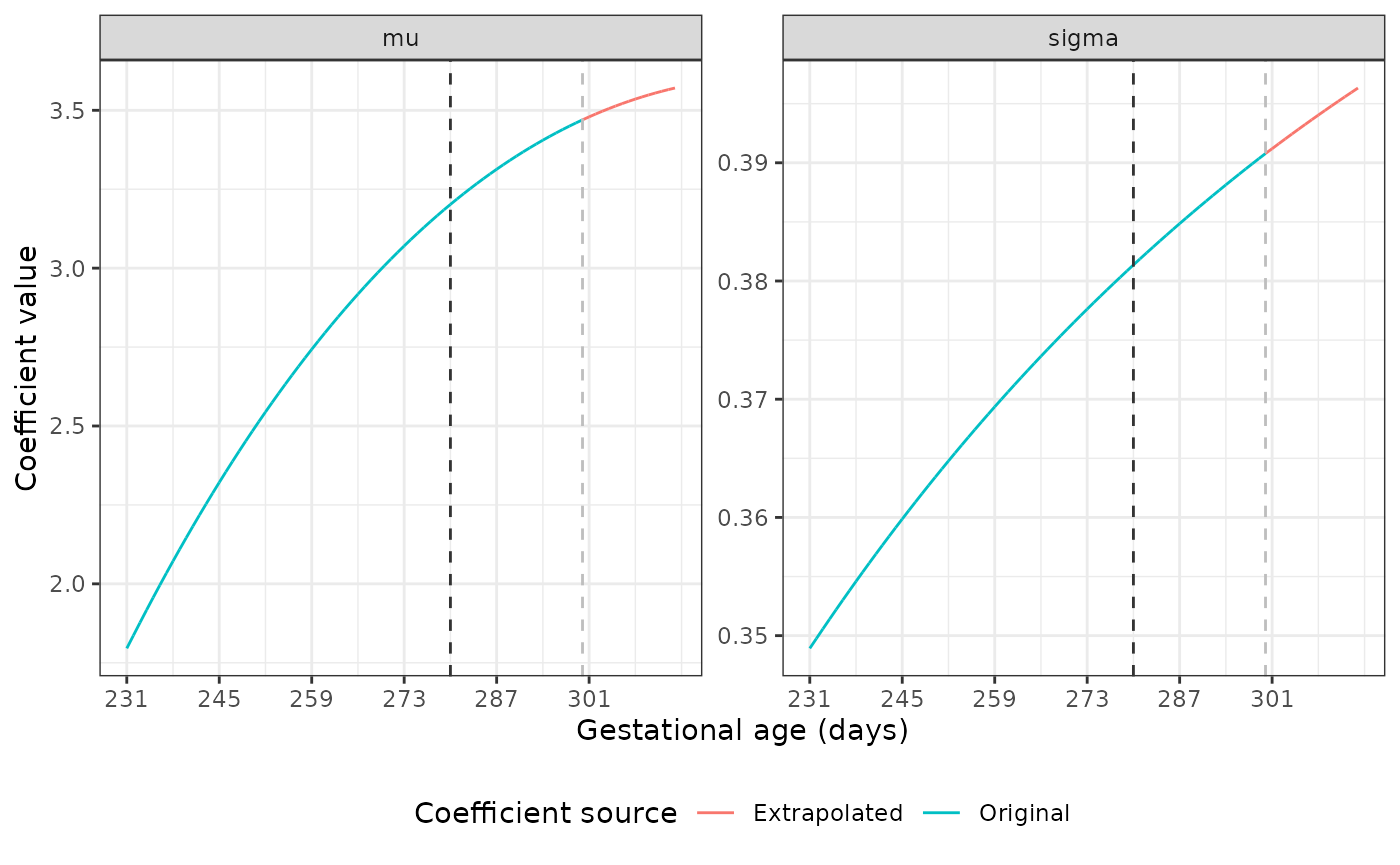
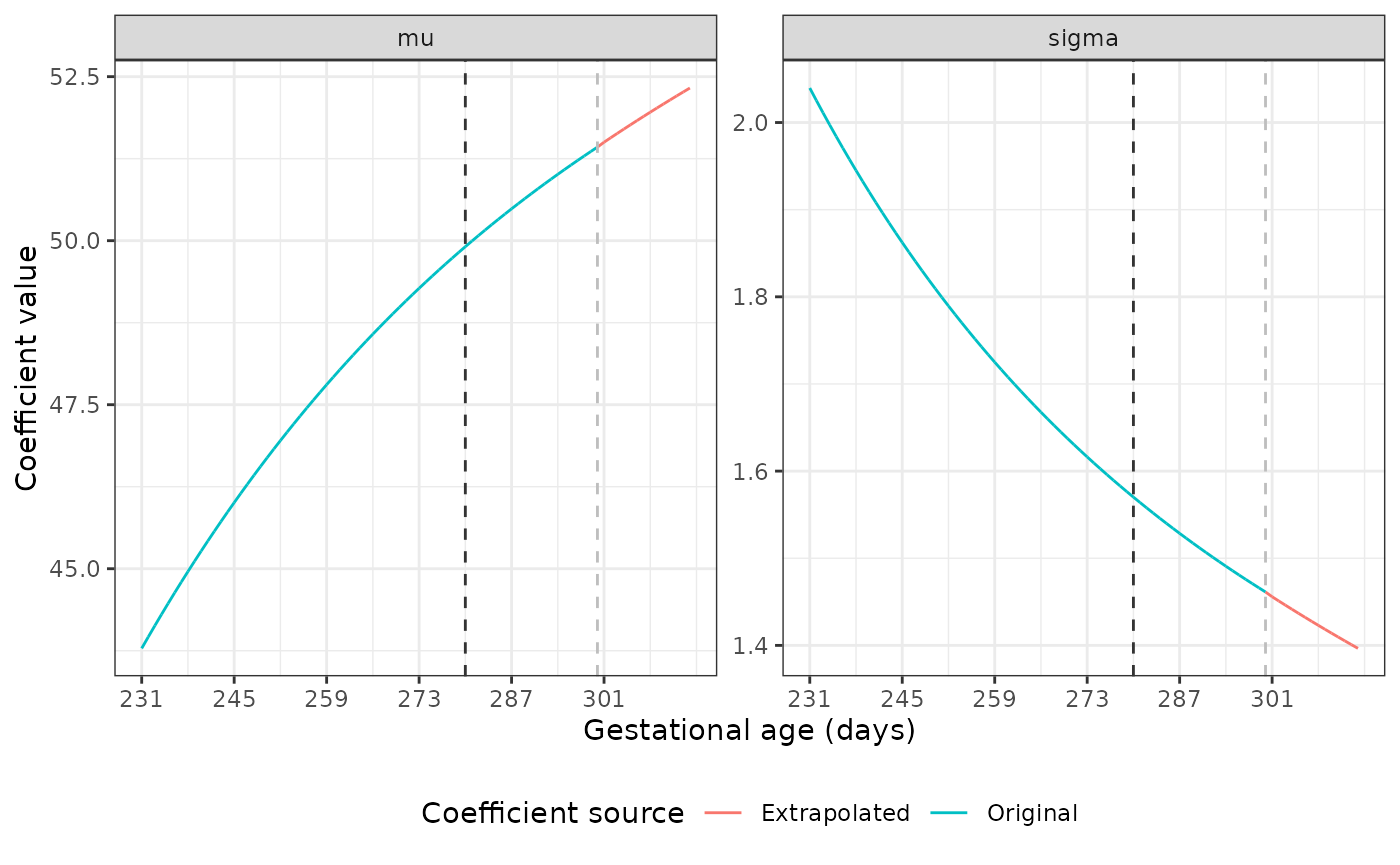
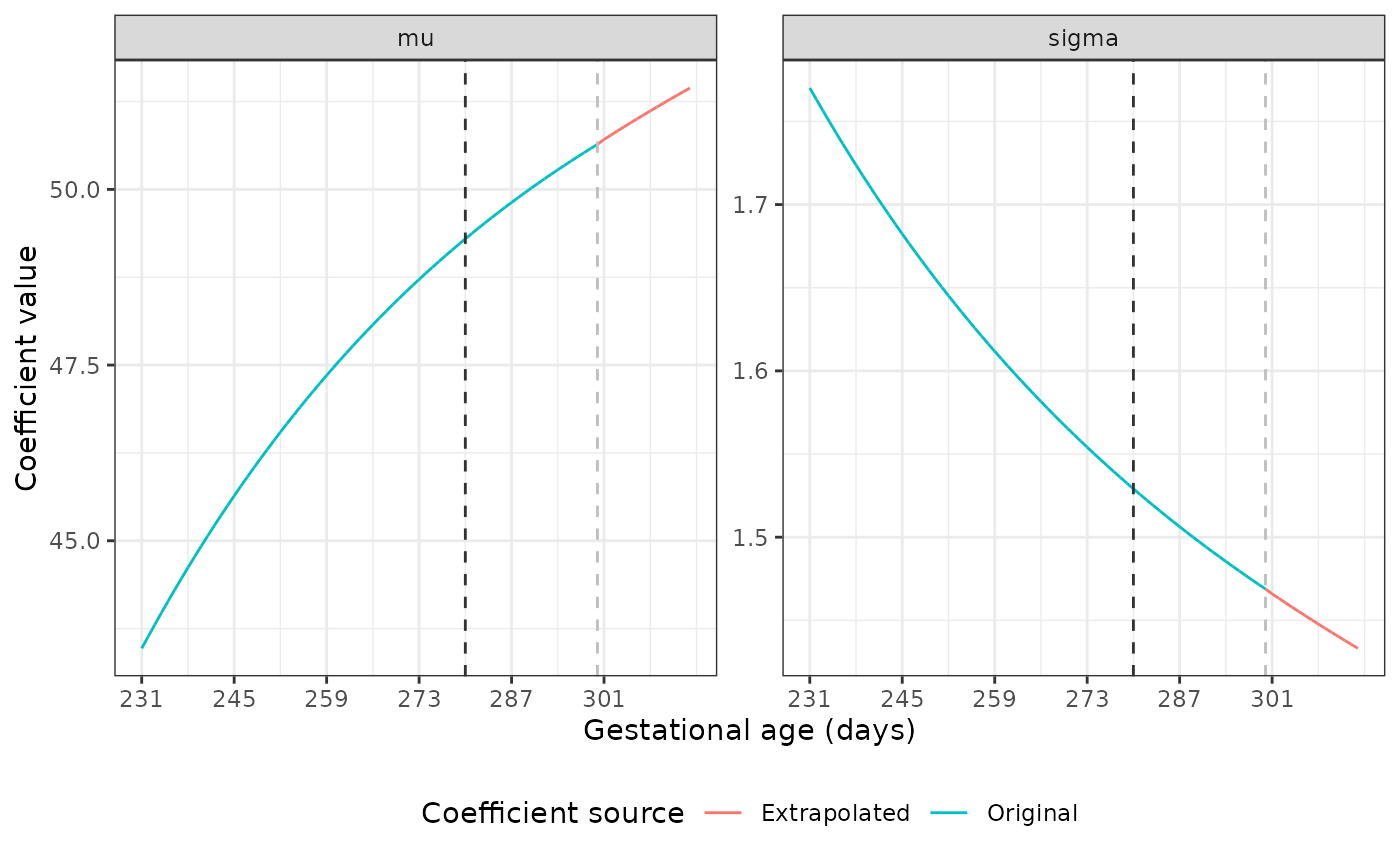
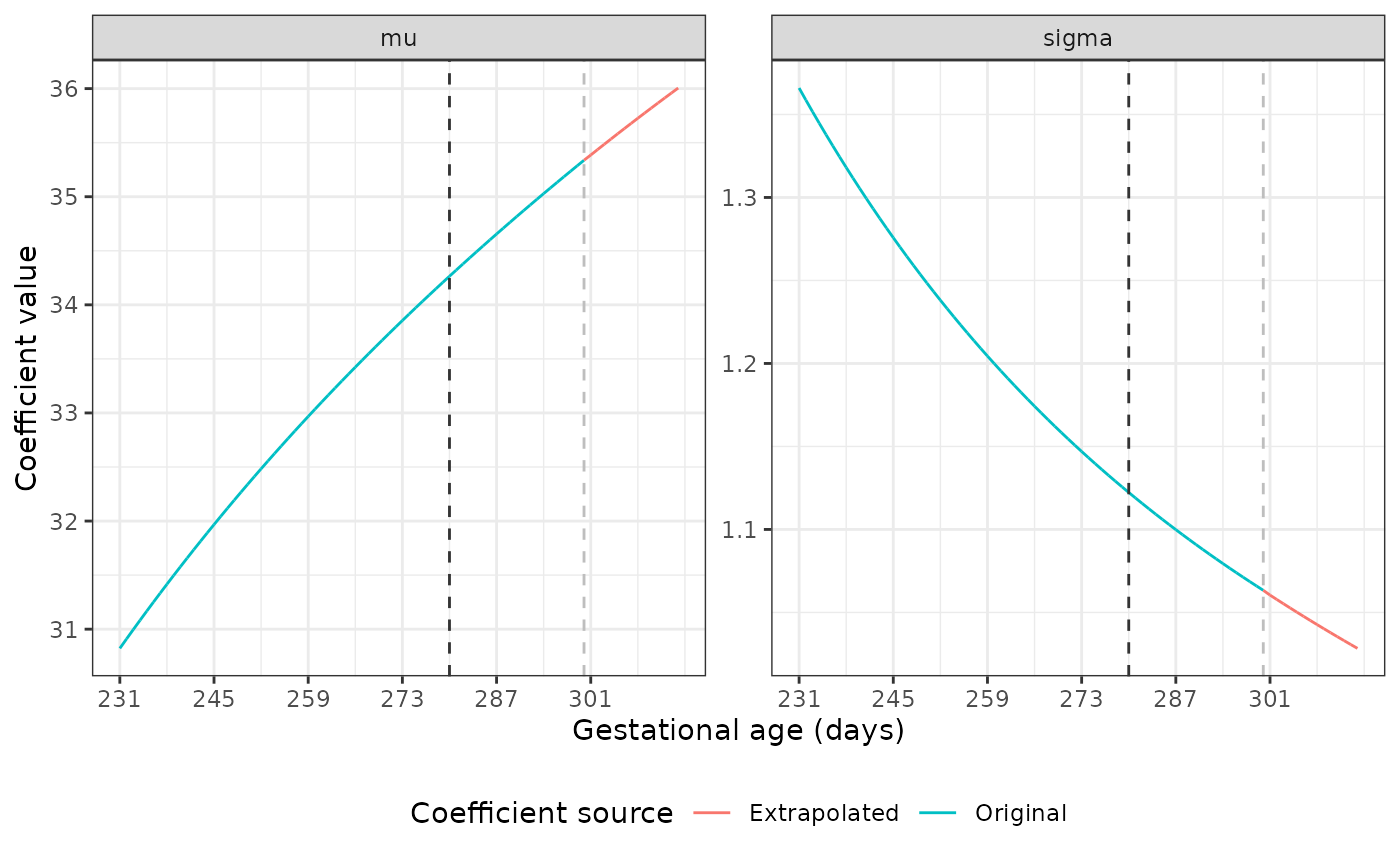
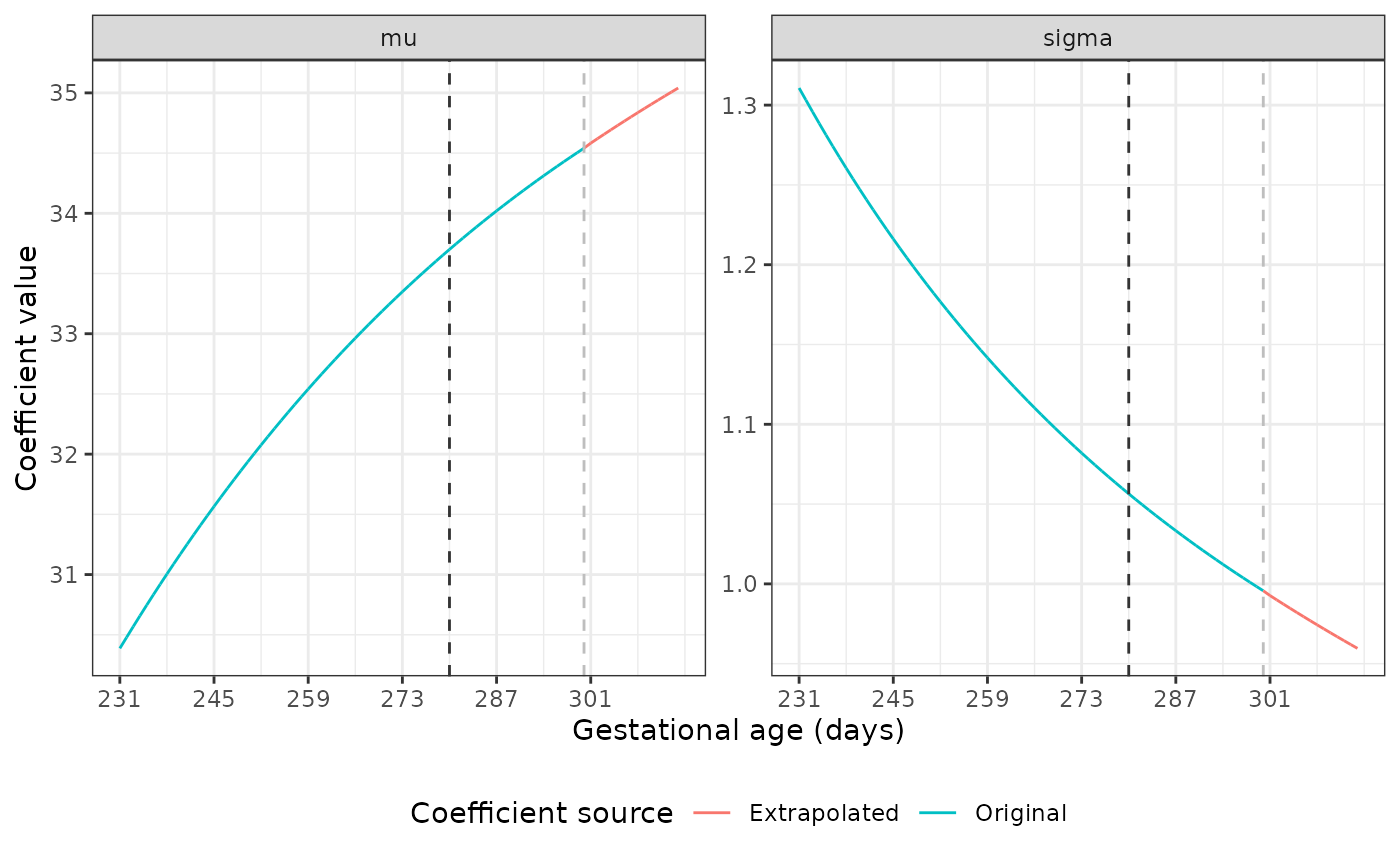
Extrapolating coefficients for the Newborn Size Standards

The mu and sigma values are different across GAs for each standard. Luckily, the nu and tau parameters are identical across all gestational ages for most of these standards. Using unique(), we see that for all INTERGROWTH-21st Newborn Size standards except female length-for-GA (lfga/female), nu and tau are constant.

#> Weight-for-GA:
#>  Male:
#>       Unique `nu` values: 1.095261
#>       Unique `tau` values: 17.05299
#>  Female:
#>       Unique `nu` values: 1.126787
#>       Unique `tau` values: 19.65738
#> 
#> Length-for-GA:
#>  Male:
#>       Unique `nu` values: 1.007603
#>       Unique `tau` values: 15.4146
#>  Female:
#>       Unique `nu` values: 0.967756, 0.9677558
#>       Unique `tau` values: 19.95849
#> 
#> Head circumference-for-GA:
#>  Male:
#>       Unique `nu` values: 1.033177
#>       Unique `tau` values: 26.17975
#>  Female:
#>       Unique `nu` values: 1.045915
#>       Unique `tau` values: 20.97268

Looking at the nu values for length-for-GA in females, we see that only the first value is different (0.9677560). Every other value in this vector is 0.9677568:

gigs::ig_nbs_coeffs$lfga$female$nu
#>  [1] 0.9677560 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#>  [8] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [15] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [22] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [29] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [36] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [43] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [50] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [57] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558
#> [64] 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558 0.9677558

We will assume for this set of coefficients that nu is equal to 0.967758 after 300 days’ GA; for all other sets of coefficients we know that nu and tau are constant throughout.

The mu and sigma parameters for each standard require extrapolation. The following function uses mfp::mfp() to model the slope of mu and sigma values against GA in each set of standards using fractional polynomials. The resulting fractional polynomial produced by can then be used with predict() to extrapolate the slopes out to 314 days’ GA.

extrapolate_msnt <- function(acronym, sex) {
  existing_coeffs <- gigs::ig_nbs_coeffs[[acronym]][[sex]]

  # Increase alpha cut-off from 0.05 to make `mfp()` 'take' to some standards
  alpha <- 0.15
  # Subset for fracpoly regresion; improves transition to >300 days vs. using
  # entire GA range
  modelling_cutoff <- 280
  modelling_coeffs <- dplyr::filter(existing_coeffs, gest_days >= modelling_cutoff)

  mfp_mu <- mfp::mfp(mu ~ fp(gest_days, df = 4), data = modelling_coeffs,
                     maxits = 200, alpha = alpha)

  coeffs_ext <- data.frame(gest_days = 231:314)
  coeffs_ext$mu <- predict(mfp_mu, newdata = coeffs_ext)

  mfp_sigma <- mfp::mfp(sigma ~ fp(gest_days, df = 4), data = modelling_coeffs,
                        maxits = 200, alpha = alpha)
  coeffs_ext$sigma <- predict(mfp_sigma, newdata = coeffs_ext)

  coeffs_ext$nu <- existing_coeffs$nu[2]
  coeffs_ext$tau <- existing_coeffs$tau[2]

  # Replace predicted coeffs with old coeffs for old GA range
  coeffs_ext$mu[seq_along(231:300)] <- existing_coeffs$mu
  coeffs_ext$sigma[seq_along(231:300)] <- existing_coeffs$sigma
  coeffs_ext
}

Let’s iterate through our different standards and sexes. We store the results in ig_nbs_ext_coeffs:

ig_nbs_ext_coeffs <- list(wfga = list(male = NULL, female = NULL),
                          lfga = list(male = NULL, female = NULL),
                          hcfga = list(male = NULL, female = NULL))

for (acronym in c("wfga", "lfga", "hcfga")) {
  for (sex in c("male", "female")) {
    ig_nbs_ext_coeffs[[acronym]][[sex]] <- extrapolate_msnt(acronym, sex)
  }
}

Plotting the extrapolated coefficients

The dark grey dashed line marks the point at which we start using the original coefficient values to fit a fractional polynomial to the data. The light grey line shows where the extrapolation begins. Our plots show good extrapolations in these coefficients.

Weight-for-GA: male

Two line graphs showing coefficient value on the y-axis by gestational age (in days) on the x-axis. At 300 days, a vertical dashed grey line indicates that extrapolation of the values of the mu and sigma coefficients begins. After this line, the value of mu and sigma change similarly to before interpolation was carried out.

Weight-for-GA: female

Two line graphs showing coefficient value on the y-axis by gestational age (in days) on the x-axis for weight-for-GA in males. At 300 days, a vertical dashed grey line indicates that extrapolation of the values of the mu and sigma coefficients begins. After this line, the value of mu and sigma change similarly to before interpolation was carried out.

Length-for-GA: male

Two line graphs showing coefficient value on the y-axis by gestational age (in days) on the x-axis for weight-for-GA in females. At 300 days, a vertical dashed grey line indicates that extrapolation of the values of the mu and sigma coefficients begins. After this line, the value of mu and sigma change similarly to before interpolation was carried out.

Length-for-GA: female

Two line graphs showing coefficient value on the y-axis by gestational age (in days) on the x-axis for length-for-GA in males. At 300 days, a vertical dashed grey line indicates that extrapolation of the values of the mu and sigma coefficients begins. After this line, the value of mu and sigma change similarly to before interpolation was carried out.

Head circumference-for-GA: male

Two line graphs showing coefficient value on the y-axis by gestational age (in days) on the x-axis for head circumference-for-GA in males. At 300 days, a vertical dashed grey line indicates that extrapolation of the values of the mu and sigma coefficients begins. After this line, the value of mu and sigma change similarly to before interpolation was carried out.

Head circumference-for-GA: female

Two line graphs showing coefficient value on the y-axis by gestational age (in days) on the x-axis for head circumference-for-GA in males. At 300 days, a vertical dashed grey line indicates that extrapolation of the values of the mu and sigma coefficients begins. After this line, the value of mu and sigma change similarly to before interpolation was carried out.

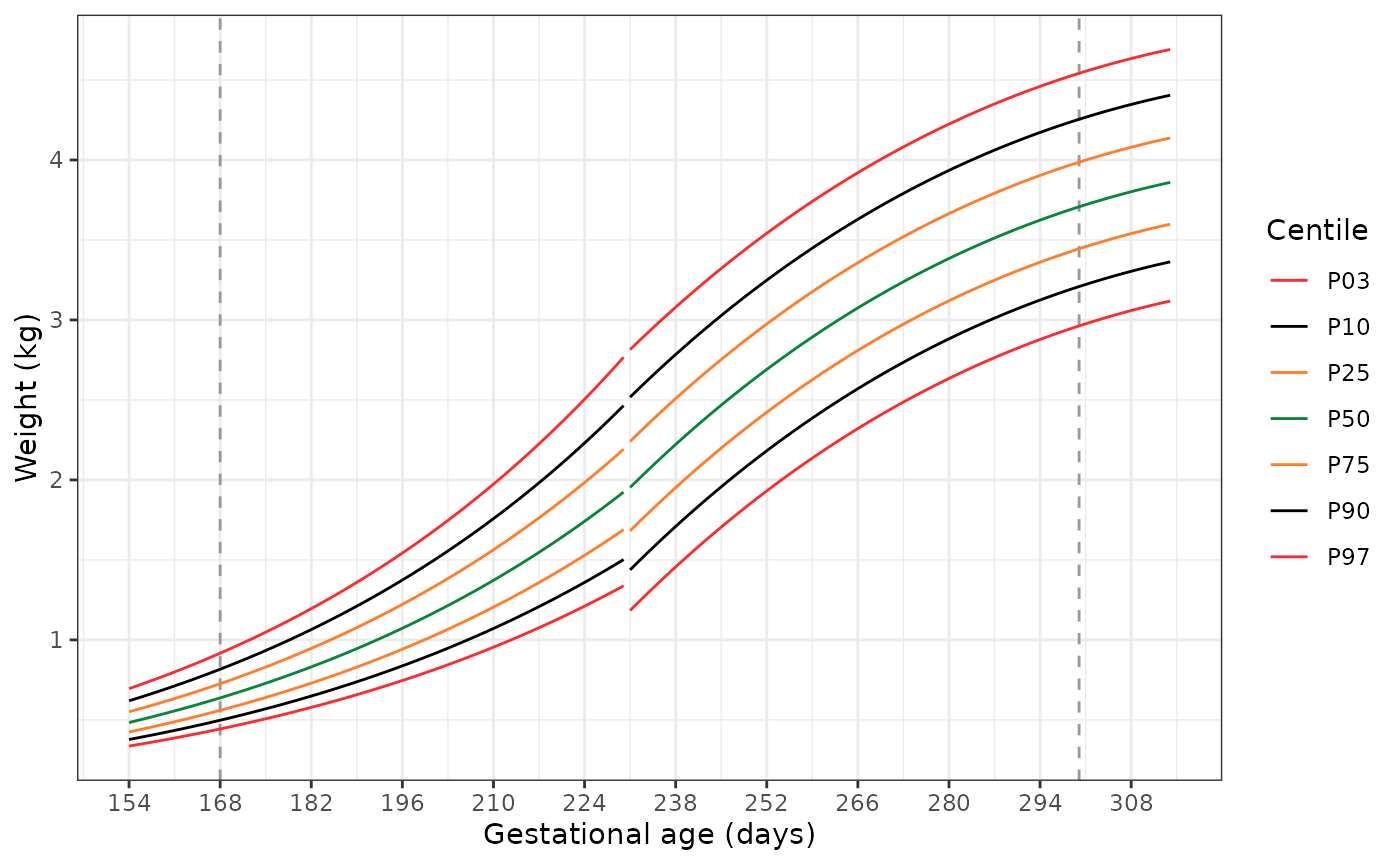
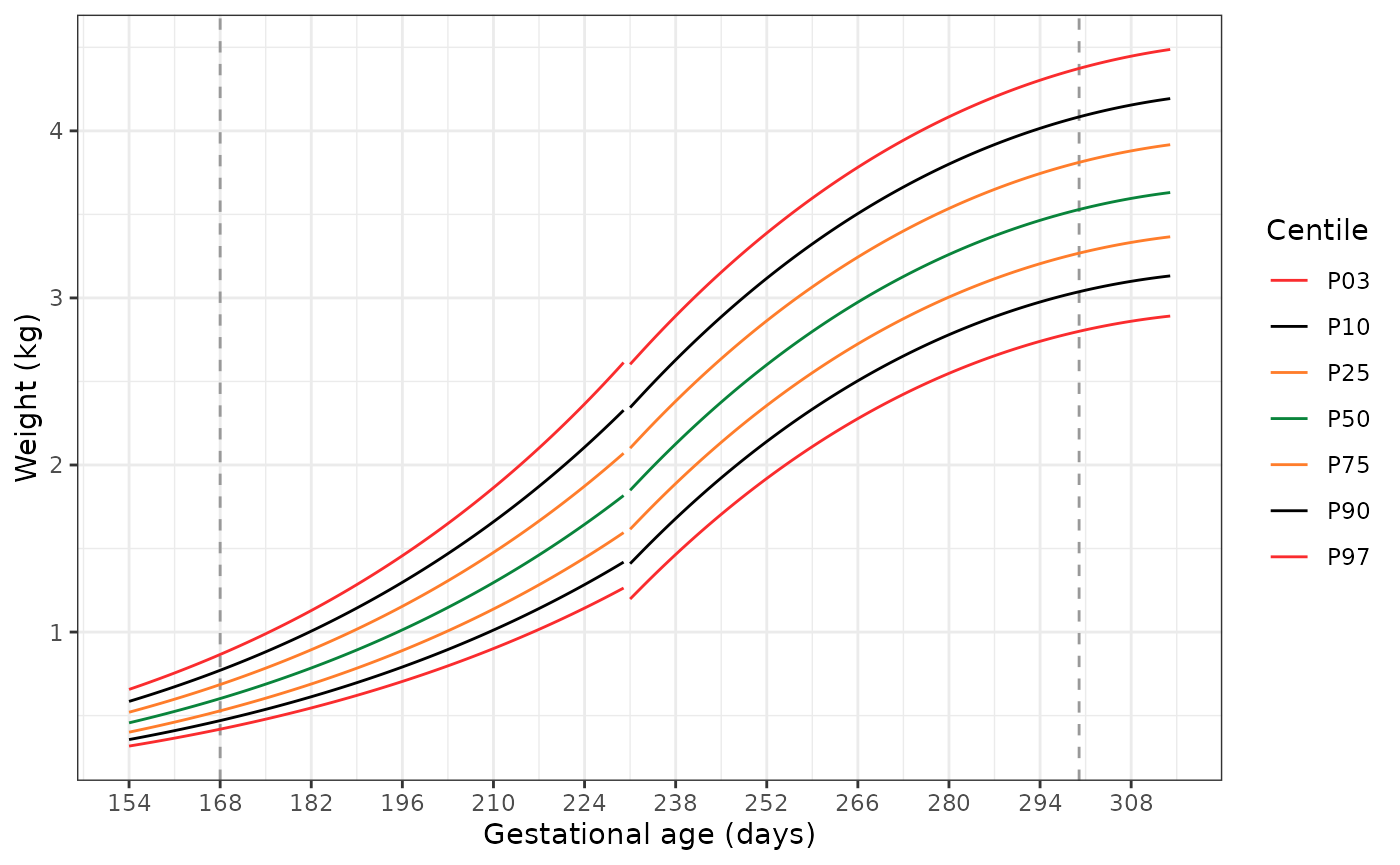
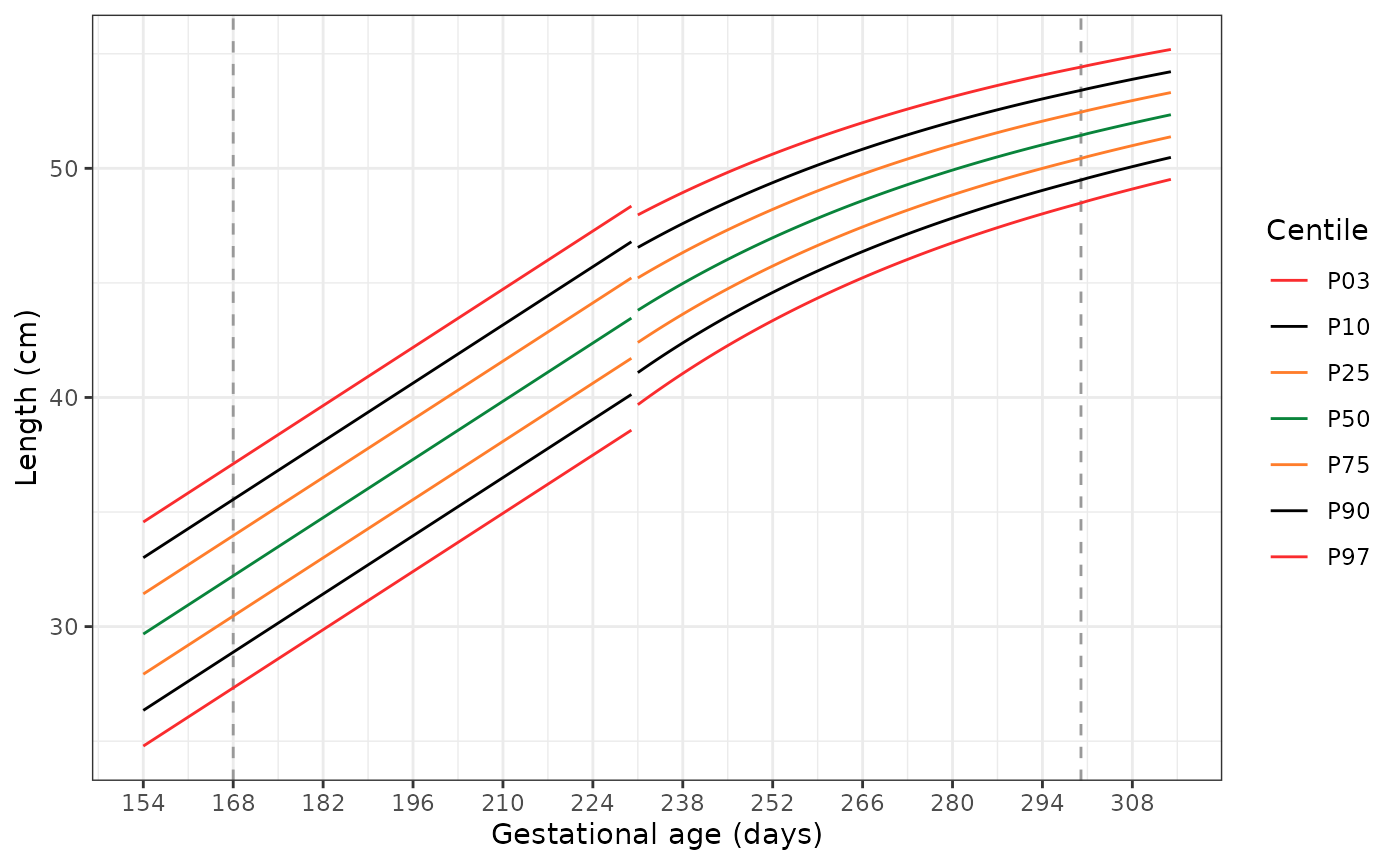
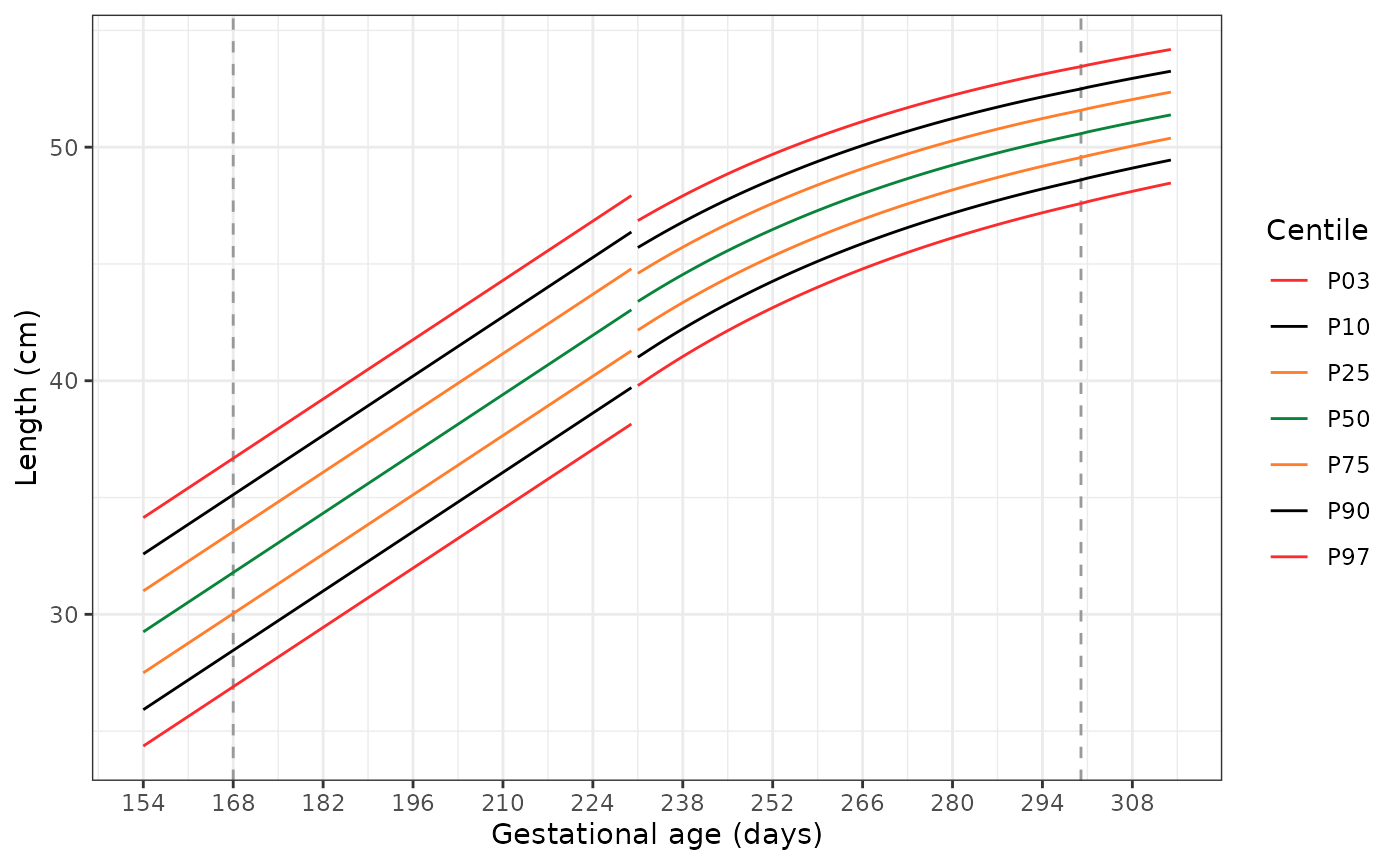
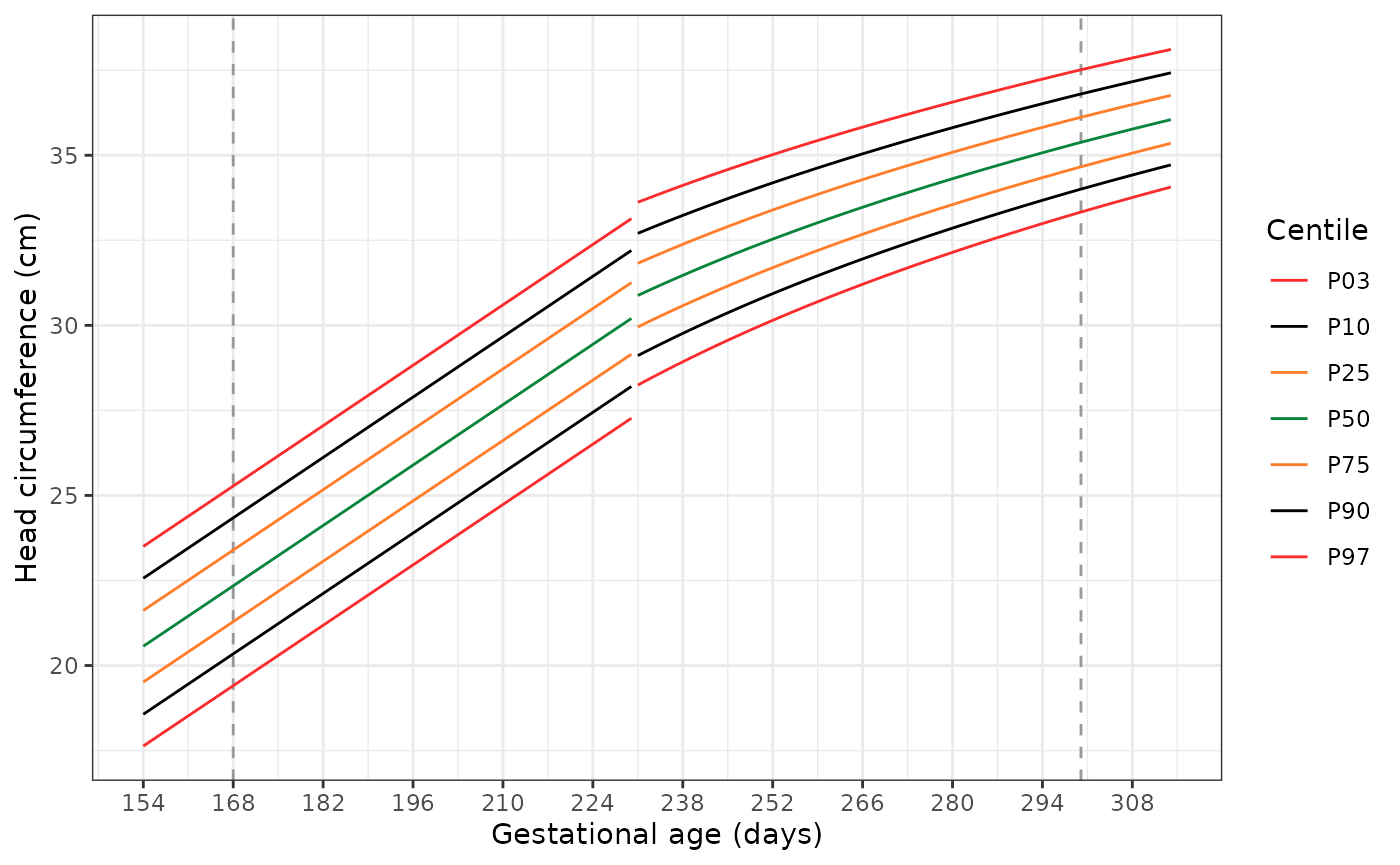
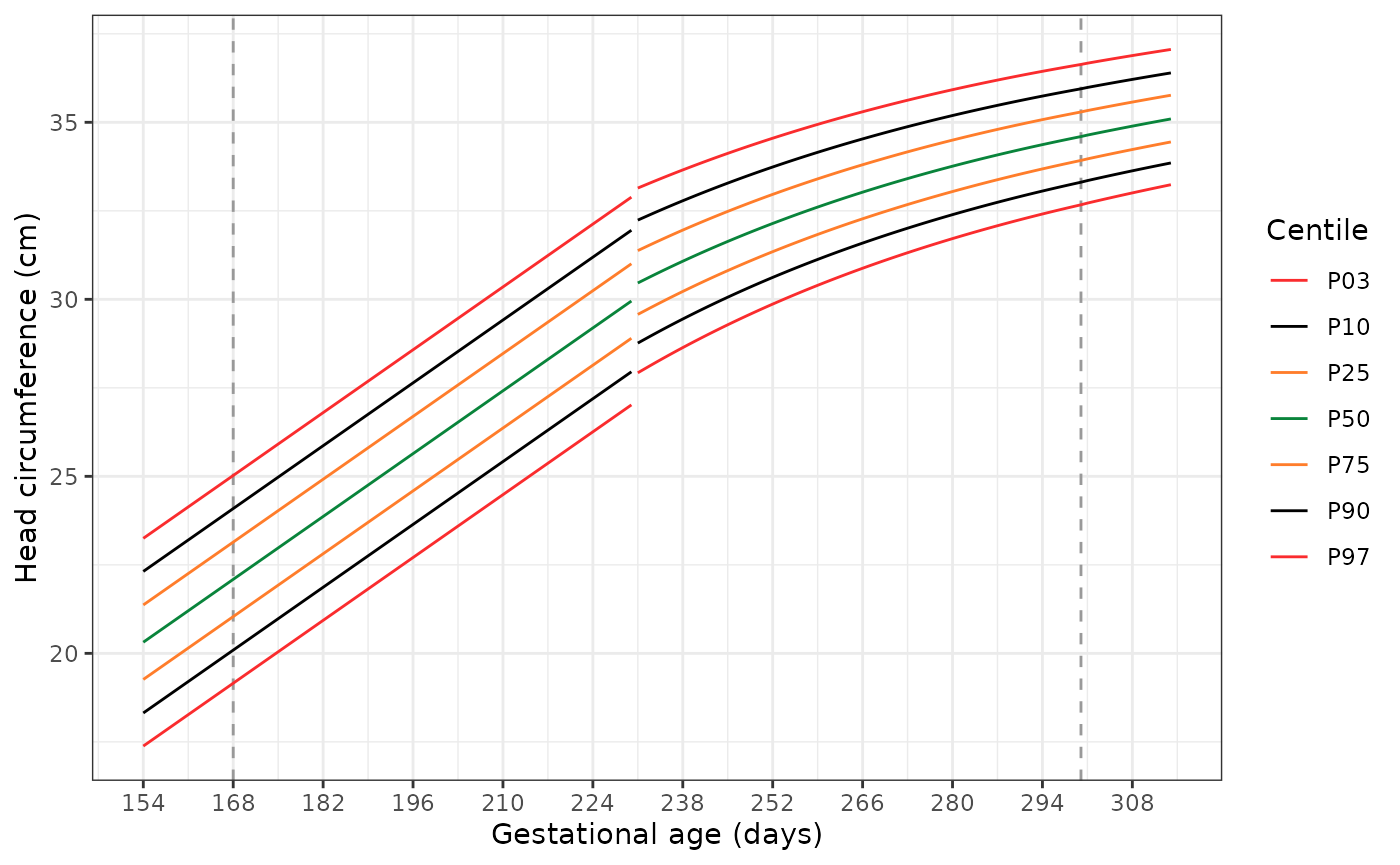
Plotting the extended standards

The following code has two functions. The first, generate_extrapolated_ig_nbs(), produces a long data frame with anthropometry for the 3rd, 10th, 25th, 50th, 75th, 90th, and 97th centiles. The second function (plot_extrapolated_ig_nbs()) uses these to graph the centiles, with grey dashed lines at 168 and 300 days to indicate where extrapolation of the INTERGROWTH-21st Very Preterm Newborn standards stops and extrapolation of the extrapolation of the INTERGROWTH-21st Newborn Size standards starts, respectively. Each plot has a gap at 231 days (33+0 weeks), where we switch from using the INTERGROWTH-21st Very Preterm standards to the INTERGROWTH-21st Newborn Size standards.

generate_extrapolated_ig_nbs <- function(acronym, sex) {
  purrr::map2(
    .x = c(0.03, 0.1, 0.25, 0.5, 0.75, 0.9, 0.97),
    .y = c("P03", "P10", "P25", "P50", "P75", "P90", "P97"),
    .f = function(centile, name) {
      vpns_lim <- 231
      gest_days <- 154:314
      y_nbs_ext <- with(ig_nbs_ext_coeffs[[acronym]][[sex]],
                        gamlss.dist::qST3C(p = centile,
                                            mu = mu,
                                            sigma = sigma,
                                            nu = nu,
                                            tau = tau))
      y_vpns_ext <- gigs:::ig_vpns_zscore2value(z = qnorm(centile),
                                                154:230,
                                                switch(sex,
                                                       male = "M",
                                                       female = "F"),
                                                acronym)
      standard <- ifelse(
        test = gest_days >= vpns_lim,
        yes = "NS",
        no = "Very Preterm NS"
      )
      x <- data.frame(gest_days = gest_days,
                      Centile = name,
                      y = c(y_vpns_ext, y_nbs_ext),
                      standard = standard)
    }) |>
    purrr::list_rbind()
}

plot_extrapolated_chart <- function(curve_data, acronym, sex) {
  key_colours <- c("P03" = "#fa2c2e",
                   "P10" = "black",
                   "P25" = "#ff7d2b",
                   "P50" = "#09843b",
                   "P75" = "#ff7d2b",
                   "P90" = "black",
                   "P97" = "#fa2c2e")
  ggplot2::ggplot(
    curve_data, ggplot2::aes(x = gest_days, y = y, colour = Centile,
                             id = standard)) +
    ggplot2::geom_vline(xintercept = 168, colour = "grey60", linetype = "dashed") +
    ggplot2::geom_vline(xintercept = 300, colour = "grey60", linetype = "dashed") +
    ggplot2::geom_line() +
    ggplot2::scale_x_continuous(breaks = seq(154, 314, 14),
                                labels = seq(154, 314, 14)) +
    ggplot2::scale_colour_manual(values = key_colours) +
    ggplot2::labs(
      x = "Gestational age (days)",
      y = switch(acronym,
                 "wfga" = "Weight (kg)",
                 "lfga" = "Length (cm)",
                 "hcfga" = "Head circumference (cm)"))
}
Weight-for-GA: male

A line graph showing the extrapolated growth curves for male weight-for-gestational age relative to the existing growth curves. Vertical light grey dashed lines indicate where extrapolation of the original INTERGROWTH-21st Newborn Size standards starts and stops. The extrapolated data (from 154 days GA to 168 days GA for the Very Preterm standards and from 301 to 314 days in the Newborn Size standards) appears to appropriately extend these standards past the existing GA bounds, at both the median (P50) and extreme centiles (P03 and P97).

Weight-for-GA: female

A line graph showing the extrapolated growth curves for female weight-for-gestational age relative to the existing growth curves. Vertical light grey dashed lines indicate where extrapolation of the original INTERGROWTH-21st Newborn Size standards starts and stops. The extrapolated data (from 154 days GA to 168 days GA for the Very Preterm standards and from 301 to 314 days in the Newborn Size standards) appears to appropriately extend these standards past the existing GA bounds, at both the median (P50) and extreme centiles (P03 and P97).

Length-for-GA: male

A line graph showing the extrapolated growth curves for male length-for-gestational age relative to the existing growth curves. Vertical light grey dashed lines indicate where extrapolation of the original INTERGROWTH-21st Newborn Size standards starts and stops. The extrapolated data (from 154 days GA to 168 days GA for the Very Preterm standards and from 301 to 314 days in the Newborn Size standards) appears to appropriately extend these standards past the existing GA bounds, at both the median (P50) and extreme centiles (P03 and P97).

Length-for-GA: female

A line graph showing the extrapolated growth curves for female length-for-gestational age relative to the existing growth curves. Vertical light grey dashed lines indicate where extrapolation of the original INTERGROWTH-21st Newborn Size standards starts and stops. The extrapolated data (from 154 days GA to 168 days GA for the Very Preterm standards and from 301 to 314 days in the Newborn Size standards) appears to appropriately extend these standards past the existing GA bounds, at both the median (P50) and extreme centiles (P03 and P97).

Head circumference-for-GA: male

A line graph showing the extrapolated growth curves for male head circumference-for-gestational age relative to the existing growth curves. Vertical light grey dashed lines indicate where extrapolation of the original INTERGROWTH-21st Newborn Size standards starts and stops. The extrapolated data (from 154 days GA to 168 days GA for the Very Preterm standards and from 301 to 314 days in the Newborn Size standards) appears to appropriately extend these standards past the existing GA bounds, at both the median (P50) and extreme centiles (P03 and P97).

Head circumference-for-GA: female

A line graph showing the extrapolated growth curves for female head circumference-for-gestational age relative to the existing growth curves. Vertical light grey dashed lines indicate where extrapolation of the original INTERGROWTH-21st Newborn Size standards starts and stops. The extrapolated data (from 154 days GA to 168 days GA for the Very Preterm standards and from 301 to 314 days in the Newborn Size standards) appears to appropriately extend these standards past the existing GA bounds, at both the median (P50) and extreme centiles (P03 and P97).

Conclusion

In all, these extrapolated versions of the Newborn Size standards (incl. Very Preterm Newborns) should be useful for researchers with large datasets that contain relatively extreme gestational ages. Anyone utilising these extended standards in their work should do so with care, and note specifically that they used the extended versions.