CANAPE example

CANAPE stands for “Categorical Analysis of Neo- And Paleo-Endemism”, and provides insight into the evolutionary processes underlying endemism (Mishler et al. 2014). The idea is basically that endemic regions may be so because either they contain range-restricted parts of a phylogeny that have unusually long branch lengths (paleoendemism), or unusually short branch lengths (neoendemism), or a mixture of both. Paleoendemism may reflect old lineages that have survived extinctions; neoendemism may reflect recently speciated lineages that have not yet dispersed.

This vignette replicates the analysis of Mishler et al. 2014, where CANAPE was originally defined.

Setup

Start by loading canaper and some other packages we will use for this vignette:

library(canaper) # This package :)
library(future) # For parallel computing
library(tictoc) # For timing things
library(patchwork) # For composing multi-part plots
# For data-wrangling and plotting
library(dplyr)
library(tidyr)
library(readr)
library(ggplot2)

Dataset

The canaper package comes with the dataset used in Mishler et al. (2014). Let’s load the data into memory:

data(acacia)

The acacia dataset is a list including two items. The first, phy, is a phylogeny of Acacia species in Australia:

acacia$phy
#> 
#> Phylogenetic tree with 510 tips and 509 internal nodes.
#> 
#> Tip labels:
#>   Pararchidendron_pruinosum, Paraserianthes_lophantha, adinophylla, semicircinalis, aphanoclada, inaequilatera, ...
#> 
#> Rooted; includes branch lengths.

The second, comm, is a community dataframe with species as columns and rows as sites. The row names (sites) correspond to the centroids of 50 x 50 km grid cells covering Australia. The community matrix is too large to print out in its entirety, so we will just take a look at the first 8 rows and columns¹:

dim(acacia$comm)
#> [1] 3037  508
acacia$comm[1:8, 1:8]
#>                   abbreviata acanthaster acanthoclada acinacea aciphylla acoma acradenia acrionastes
#> -1025000:-1825000          0           0            0        0         0     0         0           0
#> -1025000:-1875000          0           0            0        0         0     0         0           0
#> -1025000:-1925000          0           0            0        0         0     0         0           0
#> -1025000:-1975000          0           0            0        0         0     0         0           0
#> -1025000:-2025000          0           0            0        0         0     0         0           0
#> -1025000:-2075000          0           0            0        0         0     0         0           0
#> -1025000:-2125000          0           0            0        0         0     0         0           0
#> -1025000:-2225000          0           0            0        0         0     0         0           0

Randomization test

There are many metrics that describe the phylogenetic diversity of ecological communities. But how do we know if a given metric is statistically significant? One way is with a randomization test. The general process is:

Generate a set of random communities
Calculate the metric of interest for each random community
Compare the observed values to the random values

Observed values that are in the extremes (e.g, the top or lower 5% for a one-sided test, or either the top or bottom 2.5% for a two-sided test) would be considered significantly more or less diverse than random.

The main purpose of canaper is to perform these randomization tests.

canaper generates random communities using the vegan package. There are a large number of pre-defined randomization algorithms available in vegan², as well as an option to provide a user-defined algorithm. Selecting the appropriate algorithm is not trivial, and can greatly influence results³. For details about the pre-defined algorithms, see vegan::commsim().

This example also demonstrates one of the strengths of canaper: the ability to run randomizations in parallel⁴. This is by far the most time-consuming part of CANAPE, since we have to repeat the calculations many (e.g., hundreds or more) times across the randomized communities to obtain reliable results. Here, we set the number of iterations (n_iterations; i.e., the number of swaps used to produce each randomized community) fairly high because this community matrix is large and includes many zeros; thorough mixing by swapping many times is required to completely randomize the matrix.

We will use a low number of random communities (n_reps) so things finish relatively quickly; you should consider increasing n_reps for a “real” analysis⁵. We will use the curveball randomization algorithm, which maintains species richness and abundance patterns while randomizing species identity (Strona et al. 2014)⁶.

# Set a parallel back-end, with 2 CPUs running simultaneously
plan(multisession, workers = 2)

# Uncomment this to show a progress bar when running cpr_rand_test()
# progressr::handlers(global = TRUE) # nolint

# Set a random number generator seed so we get the same results if this is
# run again
set.seed(071421)

tic() # Set a timer
# Run randomization test
acacia_rand_res <- cpr_rand_test(
  acacia$comm, acacia$phy,
  null_model = "curveball",
  n_reps = 20, n_iterations = 100000,
  tbl_out = TRUE
)
#> Warning: Abundance data detected. Results will be the same as if using presence/absence data (no abundance weighting is used).
#> Warning: Dropping tips from the tree because they are not present in the community data: 
#>  Pararchidendron_pruinosum, Paraserianthes_lophantha
toc() # See how long it took
#> 70.204 sec elapsed

# Switch back to sequential (non-parallel) mode
plan(sequential)

Let’s take a peek at the output.

acacia_rand_res
#> # A tibble: 3,037 × 55
#>    site       pd_obs pd_ra…¹ pd_ra…² pd_ob…³ pd_ob…⁴ pd_ob…⁵ pd_ob…⁶ pd_ob…⁷ pd_ob…⁸ pd_al…⁹ pd_al…˟ pd_al…˟ pd_al…˟ pd_al…˟ pd_al…˟ pd_al…˟ pd_al…˟ pd_al…˟ rpd_obs rpd_r…˟ rpd_r…˟ rpd_o…˟ rpd_o…˟ rpd_o…˟ rpd_o…˟ rpd_o…˟ rpd_o…˟  pe_obs pe_ra…˟ pe_ra…˟ pe_ob…˟ pe_ob…˟ pe_ob…˟ pe_ob…˟ pe_ob…˟ pe_ob…˟
#>    <chr>       <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>
#>  1 -1025000… 0.0145   0.0207 0.00432 -1.46         1      19      20    0.05    0.95  0.0355  0.0414 0.00779  -0.753       5      14      20    0.25    0.7    0.407   0.514  0.129   -0.827       4      16      20    0.2     0.8  2.47e-5 6.14e-5 5.92e-5  -0.619       3      17      20    0.15    0.85
#>  2 -1025000… 0.0382   0.0522 0.00704 -1.99         0      20      20    0       1     0.0680  0.0883 0.00651  -3.10        0      20      20    0       1      0.561   0.595  0.0944  -0.358       9      11      20    0.45    0.55 1.44e-4 2.82e-4 1.86e-4  -0.738       5      15      20    0.25    0.75
#>  3 -1025000… 0.0378   0.0371 0.00535  0.130       12       8      20    0.6     0.4   0.0572  0.0631 0.00797  -0.743       2      17      20    0.1     0.85   0.661   0.593  0.0941   0.724      16       4      20    0.8     0.2  1.71e-4 2.42e-4 1.62e-4  -0.439       7      13      20    0.35    0.65
#>  4 -1025000… 0.0570   0.0606 0.00758 -0.480        6      14      20    0.3     0.7   0.0858  0.104  0.0105   -1.77        0      20      20    0       1      0.664   0.586  0.0913   0.863      17       3      20    0.85    0.15 5.30e-4 3.56e-4 2.33e-4   0.748      17       3      20    0.85    0.15
#>  5 -1025000… 0.0409   0.0423 0.00836 -0.176       11       9      20    0.55    0.45  0.0542  0.0713 0.00904  -1.89        0      19      20    0       0.95   0.753   0.596  0.102    1.55       19       1      20    0.95    0.05 1.25e-4 2.20e-4 1.31e-4  -0.728       6      14      20    0.3     0.7 
#>  6 -1025000… 0.00998  0.0102 0.00206 -0.0890      11       9      20    0.55    0.45  0.0276  0.0173 0.00742   1.39       18       2      20    0.9     0.1    0.361   0.695  0.337   -0.989       2      18      20    0.1     0.9  1.17e-5 3.86e-5 4.82e-5  -0.557       3      17      20    0.15    0.85
#>  7 -1025000… 0.0187   0.0230 0.00378 -1.14         3      17      20    0.15    0.85  0.0325  0.0390 0.00820  -0.782       2      16      20    0.1     0.8    0.575   0.619  0.189   -0.231      11       9      20    0.55    0.45 5.20e-5 9.07e-5 6.56e-5  -0.589       5      15      20    0.25    0.75
#>  8 -1025000… 0.0434   0.0516 0.00862 -0.955        4      16      20    0.2     0.8   0.0779  0.0956 0.00995  -1.78        1      19      20    0.05    0.95   0.557   0.544  0.100    0.125      12       8      20    0.6     0.4  4.32e-4 3.14e-4 1.24e-4   0.944      16       4      20    0.8     0.2 
#>  9 -1025000… 0.0111   0.0104 0.00172  0.418       17       3      20    0.85    0.15  0.0168  0.0211 0.00715  -0.607       6      14      20    0.3     0.7    0.662   0.558  0.227    0.461      16       4      20    0.8     0.2  2.73e-5 1.94e-5 1.53e-5   0.521      17       3      20    0.85    0.15
#> 10 -1025000… 0.0903   0.0896 0.0114   0.0601      13       7      20    0.65    0.35  0.115   0.143  0.00775  -3.51        0      20      20    0       1      0.783   0.629  0.0760   2.02       19       1      20    0.95    0.05 5.07e-4 5.76e-4 2.10e-4  -0.328      10      10      20    0.5     0.5 
#> # … with 3,027 more rows, 18 more variables: pe_alt_obs <dbl>, pe_alt_rand_mean <dbl>, pe_alt_rand_sd <dbl>, pe_alt_obs_z <dbl>, pe_alt_obs_c_upper <dbl>, pe_alt_obs_c_lower <dbl>, pe_alt_obs_q <dbl>, pe_alt_obs_p_upper <dbl>, pe_alt_obs_p_lower <dbl>, rpe_obs <dbl>, rpe_rand_mean <dbl>,
#> #   rpe_rand_sd <dbl>, rpe_obs_z <dbl>, rpe_obs_c_upper <dbl>, rpe_obs_c_lower <dbl>, rpe_obs_q <dbl>, rpe_obs_p_upper <dbl>, rpe_obs_p_lower <dbl>, and abbreviated variable names ¹pd_rand_mean, ²pd_rand_sd, ³pd_obs_z, ⁴pd_obs_c_upper, ⁵pd_obs_c_lower, ⁶pd_obs_q, ⁷pd_obs_p_upper, ⁸pd_obs_p_lower,
#> #   ⁹pd_alt_obs, ˟pd_alt_rand_mean, ˟pd_alt_rand_sd, ˟pd_alt_obs_z, ˟pd_alt_obs_c_upper, ˟pd_alt_obs_c_lower, ˟pd_alt_obs_q, ˟pd_alt_obs_p_upper, ˟pd_alt_obs_p_lower, ˟rpd_rand_mean, ˟rpd_rand_sd, ˟rpd_obs_z, ˟rpd_obs_c_upper, ˟rpd_obs_c_lower, ˟rpd_obs_q, ˟rpd_obs_p_upper, ˟rpd_obs_p_lower,
#> #   ˟pe_rand_mean, ˟pe_rand_sd, ˟pe_obs_z, ˟pe_obs_c_upper, ˟pe_obs_c_lower, ˟pe_obs_q, ˟pe_obs_p_upper, ˟pe_obs_p_lower

cpr_rand_test() produces a lot of columns. Here, pd_obs is the observed value of phylogenetic diversity (PD). Other columns starting with pd refer to aspects of the randomization: pd_rand_mean is the mean PD across the random communities, pd_rand_sd is the standard deviation of PD across the random communities, pd_obs_z is the standard effect size of PD, etc.

For details about what each column means, see cpr_rand_test().

Classify endemism

The next step in CANAPE is to classify types of endemism. For a full description, see Mishler et al. (2014). In short, this defines endemic regions based on combinations of the p-values of phylogenetic endemism (PE; pe_obs) and PE measured on an alternative tree with all branch lengths equal (pe_alt). Here is a summary borrowed from the biodiverse blog, modified to use the variables as they are defined in canaper:

If either pe_obs or pe_alt_obs are significantly high then we look for paleo- or neo-endemism
1. If rpe_obs is significantly high then we have palaeo-endemism
2. Else if rpe_obs is significantly low then we have neo-endemism
3. Else we have mixed age endemism, in which case
  1. If both pe_obs and pe_alt_obs are highly significant (p < 0.01) then we have super endemism (high in both paleo and neo)
  2. Else we have mixed (some mixture of paleo, neo and nonendemic)
Else if neither pe_obs or pe_alt_obsare significantly high then we have a non-endemic cell

cpr_classify_endem() carries this out automatically on the results from cpr_rand_test(), adding a factor called endem_type:

acacia_canape <- cpr_classify_endem(acacia_rand_res)

table(acacia_canape$endem_type)
#> 
#>           mixed             neo not significant           paleo           super 
#>              99              12            2783              68              75

Classify significance

A similar function to cpr_classify_endem() is available to classify significance of the randomization test, cpr_classify_signif(). Note that both of these take a data.frame as input and return a data.frame as output, so they are “pipe-friendly”. The second argument of cpr_classify_signif() is the name of the biodiversity metric that you want to classify. This will add a column *_signif with the significance relative to the random distribution for that metric. For example, cpr_classify_signif(df, "pd") will add the pd_signif column to df.

We can chain them together as follows:

acacia_canape <-
  cpr_classify_endem(acacia_rand_res) |>
  cpr_classify_signif("pd") |>
  cpr_classify_signif("rpd") |>
  cpr_classify_signif("pe") |>
  cpr_classify_signif("rpe")

# Take a look at one of the significance classifications:
table(acacia_canape$pd_signif)
#> 
#>          < 0.01          > 0.99 not significant 
#>             582              91            2364

Visualize results

With the randomizations and classification steps taken care of, we can now visualize the results to see how they match up with those of Mishler et al. (2014).

Note that the results will not be identical because we have used a different randomization algorithm from the paper and because of stochasticity in the random values, as well as fewer replicates for the randomization test.

Here is Figure 2, showing the results of the randomization test for PE, RPE, PE, and RPE:

# Fist do some data wrangling to make the results easier to plot
# (add lat/long columns)
acacia_canape <- acacia_canape |>
  separate(site, c("long", "lat"), sep = ":") |>
  mutate(across(c(long, lat), parse_number))

theme_update(
  panel.background = element_rect(fill = "white", color = "white"),
  panel.grid.major = element_line(color = "grey60"),
  panel.grid.minor = element_blank()
  )

a <- ggplot(acacia_canape, aes(x = long, y = lat, fill = pd_signif)) +
  geom_tile() +
  # cpr_signif_cols_2 is a CVD-friendly color palette in canaper
  scale_fill_manual(values = cpr_signif_cols_2, name = "Phylogenetic diversity") +
  guides(fill = guide_legend(title.position = "top", label.position = "bottom"))

b <- ggplot(acacia_canape, aes(x = long, y = lat, fill = rpd_signif)) +
  geom_tile() +
  scale_fill_manual(
    values = cpr_signif_cols_2, name = "Relative phylogenetic diversity"
  ) +
  guides(fill = guide_legend(title.position = "top", label.position = "bottom"))

c <- ggplot(acacia_canape, aes(x = long, y = lat, fill = pe_signif)) +
  geom_tile() +
  scale_fill_manual(values = cpr_signif_cols_2, name = "Phylogenetic endemism") +
  guides(fill = guide_legend(title.position = "top", label.position = "bottom"))

d <- ggplot(acacia_canape, aes(x = long, y = lat, fill = rpe_signif)) +
  geom_tile() +
  scale_fill_manual(
    values = cpr_signif_cols_2, name = "Relative phylogenetic endemism"
  ) +
  guides(fill = guide_legend(title.position = "top", label.position = "bottom"))

a + b + c + d +
  plot_annotation(tag_levels = "a") & theme(legend.position = "top")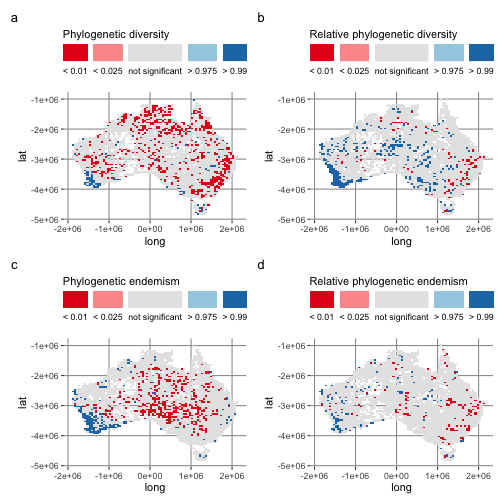

Significance results

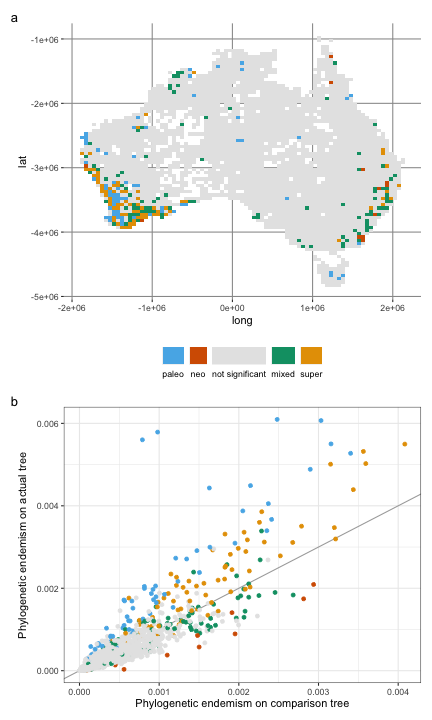
And here is Figure 3, showing the results of CANAPE:

a <- ggplot(acacia_canape, aes(x = long, y = lat, fill = endem_type)) +
  geom_tile() +
  # cpr_endem_cols_4 is a CVD-friendly color palette in canaper
  scale_fill_manual(values = cpr_endem_cols_4) +
  guides(
    fill = guide_legend(title.position = "top", label.position = "bottom")
  ) +
  theme(legend.position = "bottom", legend.title = element_blank())

b <- ggplot(
  acacia_canape,
  aes(x = pe_alt_obs, y = pe_obs, color = endem_type)
) +
  geom_abline(slope = 1, color = "darkgrey") +
  geom_point() +
  scale_color_manual(values = cpr_endem_cols_4) +
  labs(
    x = "Phylogenetic endemism on comparison tree",
    y = "Phylogenetic endemism on actual tree"
  ) +
  theme_bw() +
  theme(legend.position = "none")

a + b + plot_layout(ncol = 1) + plot_annotation(tag_levels = "a")

CANAPE results

References

Mishler, Brent D, Nunzio Knerr, Carlos E. González-Orozco, Andrew H. Thornhill, Shawn W. Laffan, and Joseph T. Miller. 2014. “Phylogenetic Measures of Biodiversity and Neo- and Paleo-Endemism in Australian Acacia.” Nature Communications 5: 4473. https://doi.org/10.1038/ncomms5473.

Strona, Giovanni, Domenico Nappo, Francesco Boccacci, Simone Fattorini, and Jesus San-Miguel-Ayanz. 2014. “A Fast and Unbiased Procedure to Randomize Ecological Binary Matrices with Fixed Row and Column Totals.” Nature Communications 5 (1): 4114. https://doi.org/10.1038/ncomms5114.

Strona, Giovanni, Werner Ulrich, and Nicholas J. Gotelli. 2018. “Bi‐dimensional Null Model Analysis of Presence‐absence Binary Matrices.” Ecology 99 (1): 103–15. https://doi.org/10.1002/ecy.2043.

Joel H. Nitta

05 April, 2023