Skip to contents

Simulate the number of iterations needed to generate a random community that is sufficiently different from the original community

Source: R/cpr_iter_sim.R
cpr_iter_sim.Rd

For randomization algorithms that involve swapping (iterations), there is no way to know a-priori how many iterations are needed to sufficiently "mix" the community data matrix. cpr_iter_sim() records the percentage similarity between the original matrix and a matrix that has been randomized with successive swapping iterations, at each iteration.

Usage

cpr_iter_sim(
  comm,
  null_model = "curveball",
  n_iterations = 100,
  thin = 1,
  seed = NULL
)

Arguments

comm

Dataframe or matrix; input community data with sites (communities) as rows and species as columns. Values of each cell are the presence/absence (0 or 1) or number of individuals (abundance) of each species in each site.

null_model

Character vector of length 1 or object of class commsim; either the name of the model to use for generating random communities (null model), or a custom null model. For full list of available predefined null models, see the help file of vegan::commsim(), or run vegan::make.commsim(). An object of class commsim can be generated with vegan::commsim().

n_iterations

Numeric vector of length 1; maximum number of iterations to conduct.

thin

Numeric vector of length 1; frequency to record percentage similarity between original matrix and randomized matrix. Results will be recorded every thin iterations (see Details).

seed

Integer vector of length 1 or NULL; random seed that will be used in a call to set.seed() before randomizing the matrix. Default (NULL) will not change the random generator state.

Value

Tibble (dataframe) with the following columns:

  • iteration: Number of iterations used to generate random community

  • similarity: Percentage similarity between original community and random community

Details

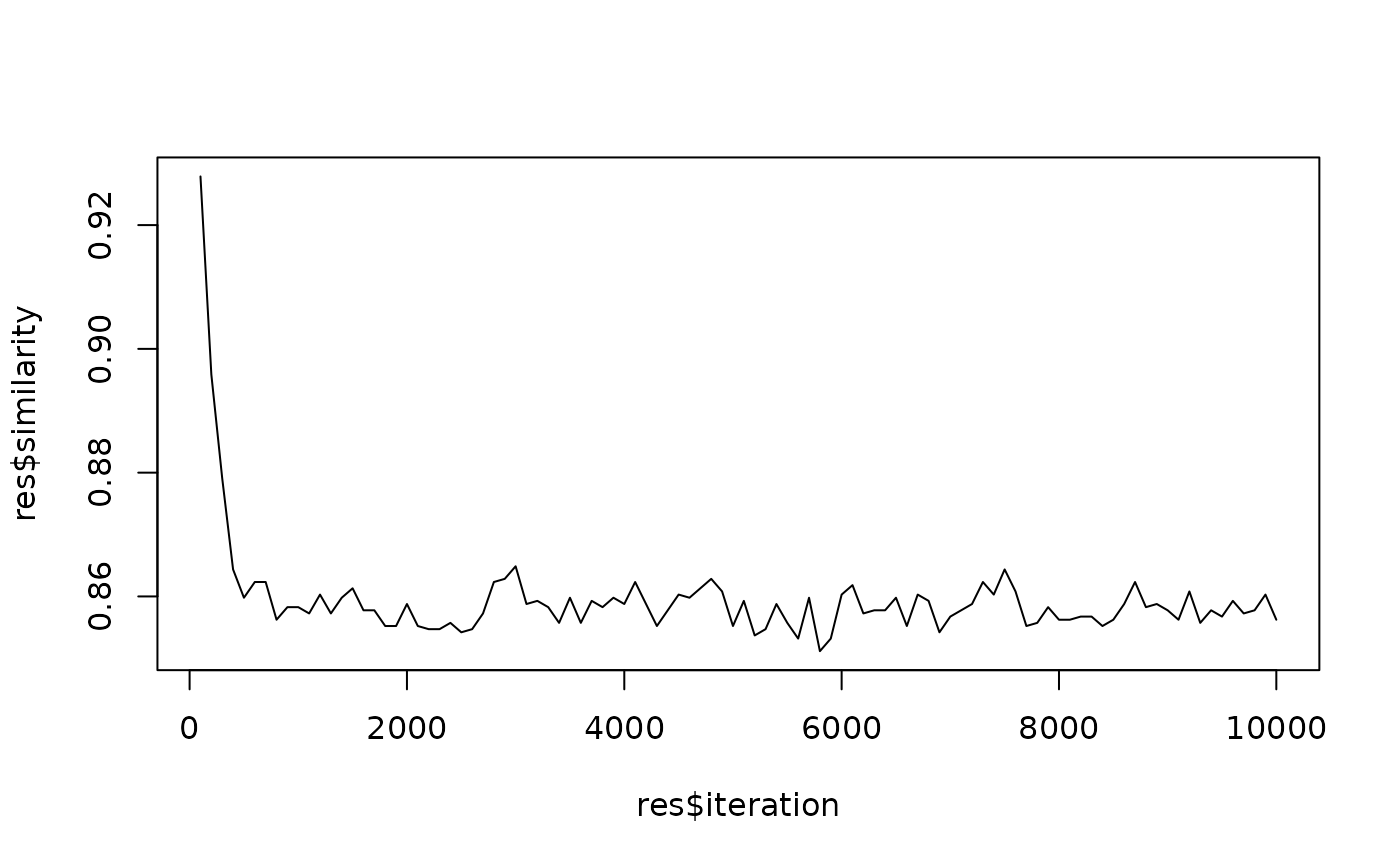
The user should inspect the results to determine at what number of iterations the original matrix and randomized matrix reach maximum dissimilarity (see Examples). This number will strongly depend on the size and structure of the original matrix. Large matrices with many zeros will likely take more iterations, and even then still retain relatively high similarity between the original matrix and the randomized matrix.

Available memory may be quickly exhausted if many (e.g., tens or hundreds of thousands, or more) of iterations are used with no thinning on large matrices; use thin to only record a portion of the results and save on memory.

Of course, cpr_iter_sim() only makes sense for randomization algorithms that use iterations.

Only presence/absence information is used to calculate percentage similarity between community matrices.

Examples

# Simulate generation of a random community with maximum of 10,000
# iterations, recording similarity every 100 iterations
(res <- cpr_iter_sim(
  comm = biod_example$comm,
  null_model = "swap",
  n_iterations = 10000,
  thin = 100,
  seed = 123
))
#> # A tibble: 100 × 2
#>    iteration similarity
#>        <int>      <dbl>
#>  1       100      0.928
#>  2       200      0.896
#>  3       300      0.879
#>  4       400      0.864
#>  5       500      0.860
#>  6       600      0.862
#>  7       700      0.862
#>  8       800      0.856
#>  9       900      0.858
#> 10      1000      0.858
#> # ℹ 90 more rows

# Plot reveals that ca. 1000 iterations are sufficient to
# completely mix random community
plot(res$iteration, res$similarity, type = "l")