Performance

Eunseop Kim

All the tests were done on an Arch Linux x86_64 machine with an Intel(R) Core(TM) i7 CPU (1.90GHz).

Empirical likelihood computation

We show the performance of computing empirical likelihood with el_mean(). We test the computation speed with simulated data sets in two different settings: 1) the number of observations increases with the number of parameters fixed, and 2) the number of parameters increases with the number of observations fixed.

Increasing the number of observations

We fix the number of parameters at $p = 10$, and simulate the parameter value and $n \times p$ matrices using rnorm(). In order to ensure convergence with a large $n$, we set a large threshold value using el_control().

library(ggplot2)
library(microbenchmark)
set.seed(3175775)
p <- 10
par <- rnorm(p, sd = 0.1)
ctrl <- el_control(th = 1e+10)
result <- microbenchmark(
  n1e2 = el_mean(matrix(rnorm(100 * p), ncol = p), par = par, control = ctrl),
  n1e3 = el_mean(matrix(rnorm(1000 * p), ncol = p), par = par, control = ctrl),
  n1e4 = el_mean(matrix(rnorm(10000 * p), ncol = p), par = par, control = ctrl),
  n1e5 = el_mean(matrix(rnorm(100000 * p), ncol = p), par = par, control = ctrl)
)

Below are the results:

result
#> Unit: microseconds
#>  expr        min         lq        mean      median          uq        max
#>  n1e2    447.205    486.254    525.1408    505.1695    573.3065    639.906
#>  n1e3   1242.714   1408.559   1532.4583   1507.2885   1626.6765   2582.548
#>  n1e4  10847.710  12445.111  14628.1767  15071.0550  16124.2235  19346.727
#>  n1e5 173354.969 202472.709 242520.7464 234432.1965 259868.0575 400198.154
#>  neval cld
#>    100 a  
#>    100 a  
#>    100  b 
#>    100   c
autoplot(result)
#> Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
#> ℹ Please use tidy evaluation idioms with `aes()`.
#> ℹ See also `vignette("ggplot2-in-packages")` for more information.
#> ℹ The deprecated feature was likely used in the microbenchmark package.
#>   Please report the issue at
#>   <https://github.com/joshuaulrich/microbenchmark/issues/>.
#> This warning is displayed once per session.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.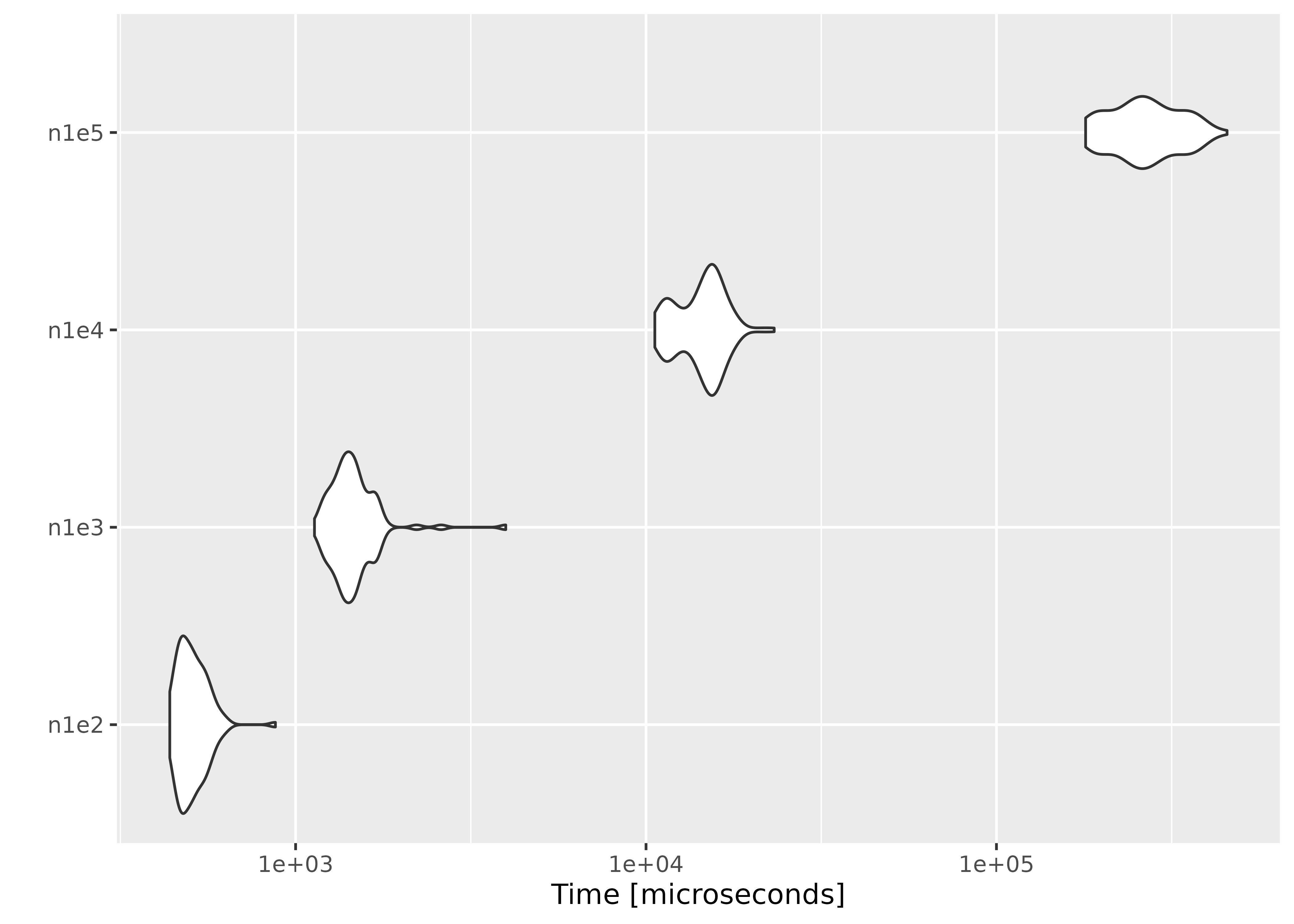

Increasing the number of parameters

This time we fix the number of observations at $n = 1000$, and evaluate empirical likelihood at zero vectors of different sizes.

n <- 1000
result2 <- microbenchmark(
  p5 = el_mean(matrix(rnorm(n * 5), ncol = 5),
    par = rep(0, 5),
    control = ctrl
  ),
  p25 = el_mean(matrix(rnorm(n * 25), ncol = 25),
    par = rep(0, 25),
    control = ctrl
  ),
  p100 = el_mean(matrix(rnorm(n * 100), ncol = 100),
    par = rep(0, 100),
    control = ctrl
  ),
  p400 = el_mean(matrix(rnorm(n * 400), ncol = 400),
    par = rep(0, 400),
    control = ctrl
  )
)

result2
#> Unit: microseconds
#>  expr        min          lq        mean      median          uq        max
#>    p5    725.847    767.1845    820.8142    802.1845    846.7885   1482.451
#>   p25   2895.253   2949.8145   3049.8471   2983.7680   3047.2170   6089.104
#>  p100  23415.755  25950.9240  28376.1969  26387.1750  30999.7225  49459.272
#>  p400 268970.349 292313.7685 327537.1182 315001.4870 341523.3385 531163.398
#>  neval cld
#>    100 a  
#>    100 a  
#>    100  b 
#>    100   c
autoplot(result2)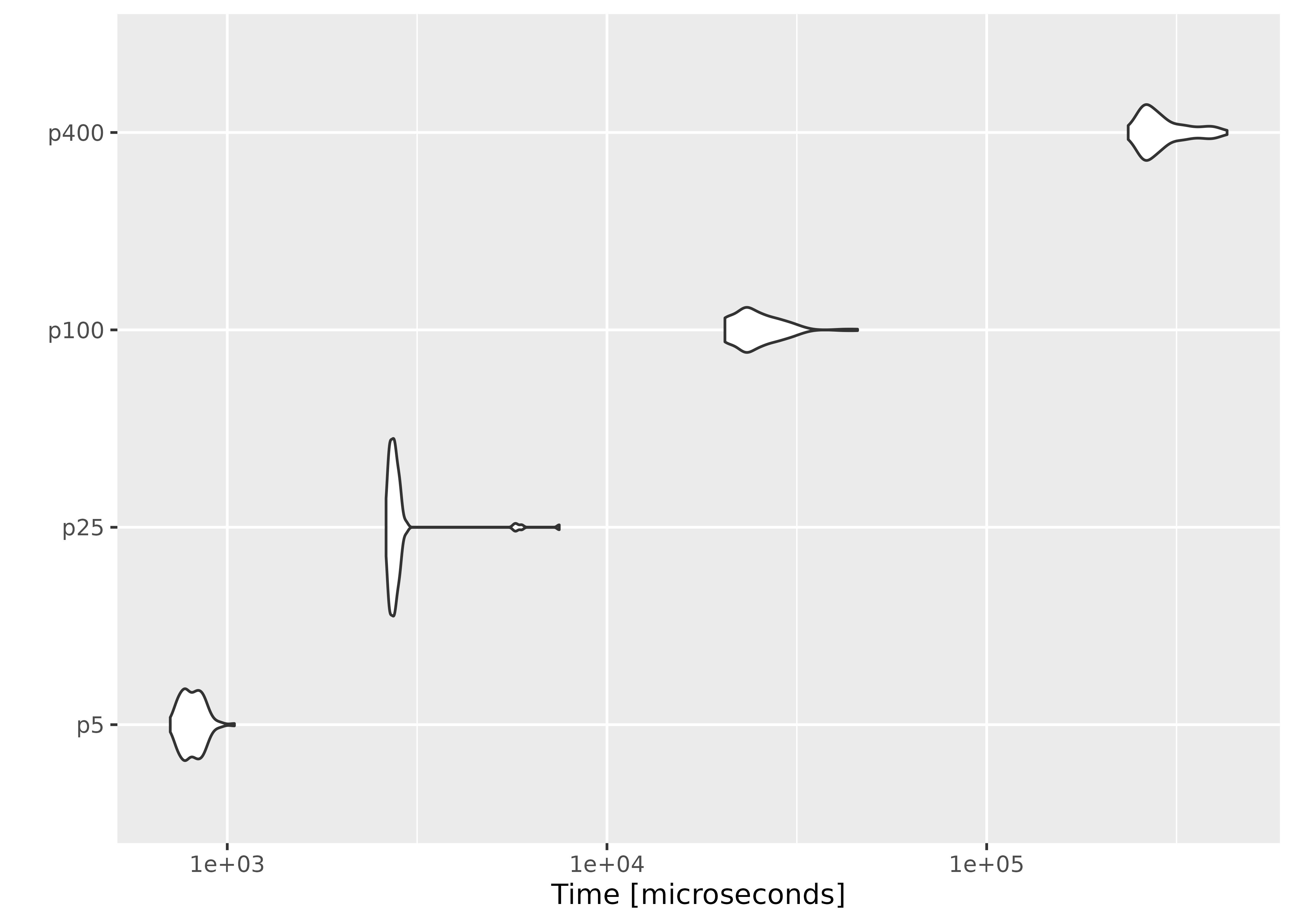

On average, evaluating empirical likelihood with a 100000×10 or 1000×400 matrix at a parameter value satisfying the convex hull constraint takes less than a second.