Skip to contents

Summarising results from predictNMB

Source: vignettes/summarising-results-with-predictNMB.Rmd
summarising-results-with-predictNMB.Rmd

This vignette is purely about how to use the autoplot() method and summary() to visualise and summarise the simulations made using predictNMB. For an introduction to predictNMB, please see the introductory vignette.

Firstly, as an example case, we will prepare our sampling functions and run screen_simulation_inputs().

get_nmb_sampler_training <- get_nmb_sampler(
  wtp = 28033,
  qalys_lost = function() rnorm(n = 1, mean = 0.0036, sd = 0.0005),
  high_risk_group_treatment_cost = function() rnorm(n = 1, mean = 20, sd = 3),
  high_risk_group_treatment_effect = function() rbeta(n = 1, shape1 = 40, shape2 = 60),
  use_expected_values = TRUE
)

get_nmb_sampler_evaluation <- get_nmb_sampler(
  wtp = 28033,
  qalys_lost = function() rnorm(n = 1, mean = 0.0036, sd = 0.0005),
  high_risk_group_treatment_cost = function() rnorm(n = 1, mean = 20, sd = 3),
  high_risk_group_treatment_effect = function() rbeta(n = 1, shape1 = 40, shape2 = 60)
)
cl <- makeCluster(2)
sim_screen_obj <- screen_simulation_inputs(
  n_sims = 500,
  n_valid = 10000,
  sim_auc = seq(0.7, 0.95, 0.05),
  event_rate = c(0.1, 0.2),
  fx_nmb_training = get_nmb_sampler_training,
  fx_nmb_evaluation = get_nmb_sampler_evaluation,
  cutpoint_methods = c("all", "none", "youden", "value_optimising"),
  cl = cl
)
stopCluster(cl)

Making plots with predictNMB

Plotting the results from screen_simulation_inputs()

Choosing the x-axis variable and other constants

In this simulation screen, we vary both the event rate and the model discrimination (sim_AUC). There are many ways that we could visualise the data. The autoplot() function allows us to make some basic plots to compare the impact of different cutpoint methods on Net Monetary Benefit (NMB) and another variable of our choice.

In this case, we can visualise the impact on NMB for different methods across varying levels of sim_auc or event_rate. We control this with the x_axis_var argument.

autoplot(sim_screen_obj, x_axis_var = "sim_auc")
#> 
#> 
#> Varying simulation inputs, other than sim_auc, are being held constant:
#> event_rate: 0.1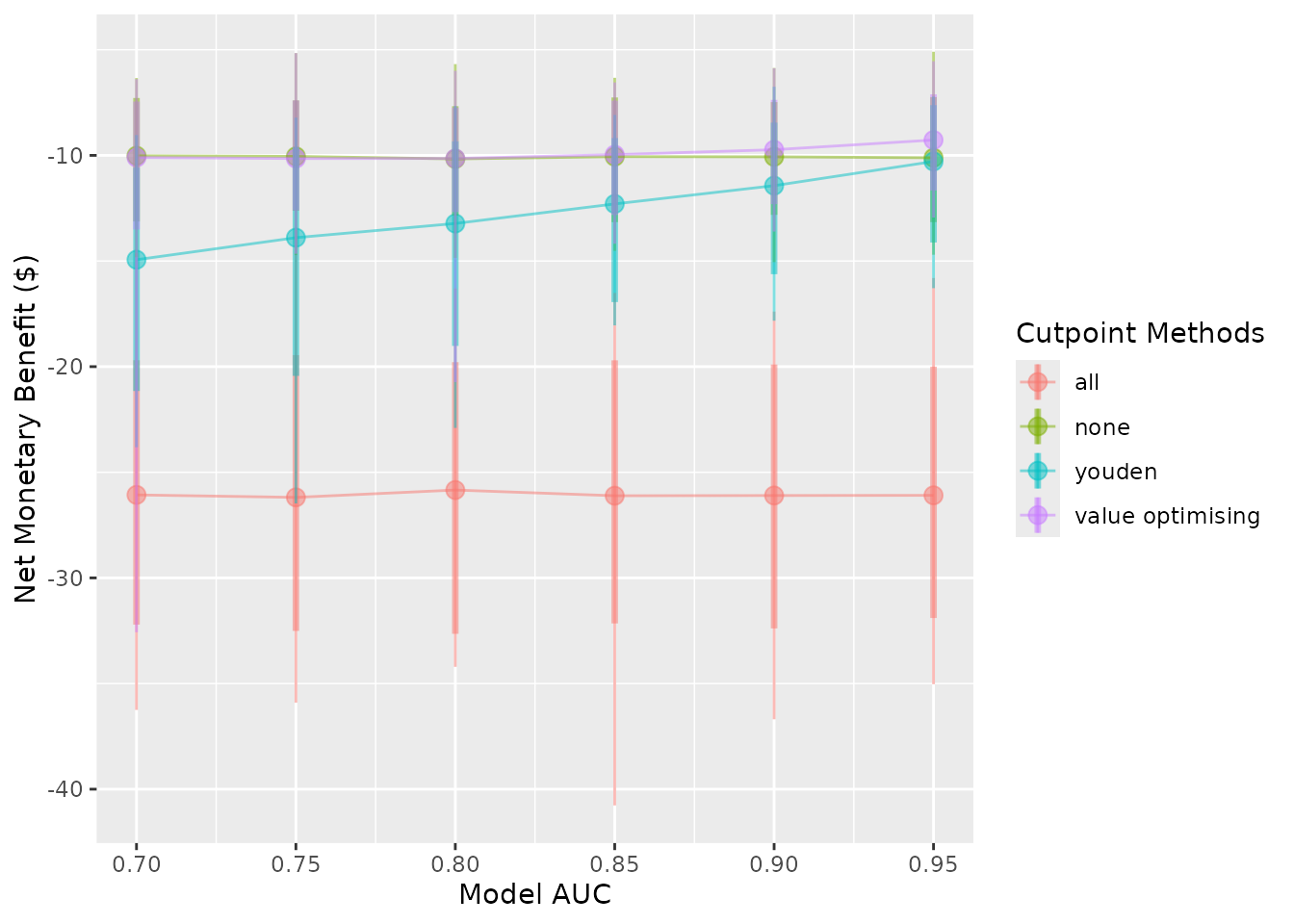

To avoid the overlap of points in this second plot, which visualises NMB at varying event rates, we can specify the dodge_width to be non-zero.

autoplot(sim_screen_obj, x_axis_var = "event_rate", dodge_width = 0.002)
#> 
#> 
#> Varying simulation inputs, other than event_rate, are being held constant:
#> sim_auc: 0.7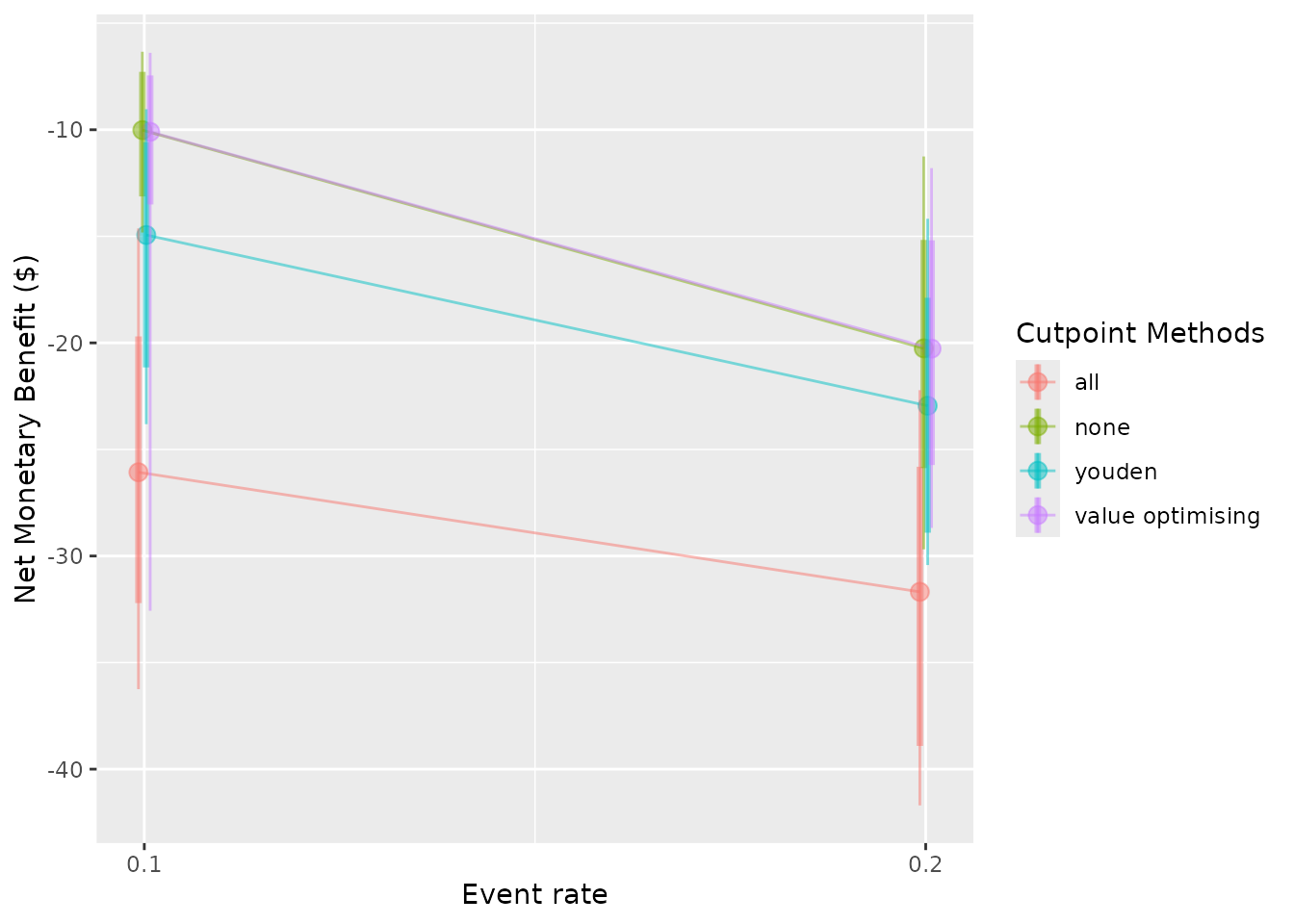

For these plots, one of the screened inputs will be the x-axis variable, but the other will only be displayed at a single level. For example, if we are looking at outcomes over a range of AUC values, the prevalence will be fixed. The default setting for this second input will assume the first level, so when we visualise the change in NMB specifying sim_auc as the x-axis variable, we only observe this for the case where event_rate = 0.1. We can choose to select another level with the constants argument. This argument expects a named list containing the values to keep for the screened inputs which are not shown on the x-axis.

autoplot(sim_screen_obj, x_axis_var = "sim_auc", constants = list(event_rate = 0.1))
#> 
#> 
#> Varying simulation inputs, other than sim_auc, are being held constant:
#> event_rate: 0.1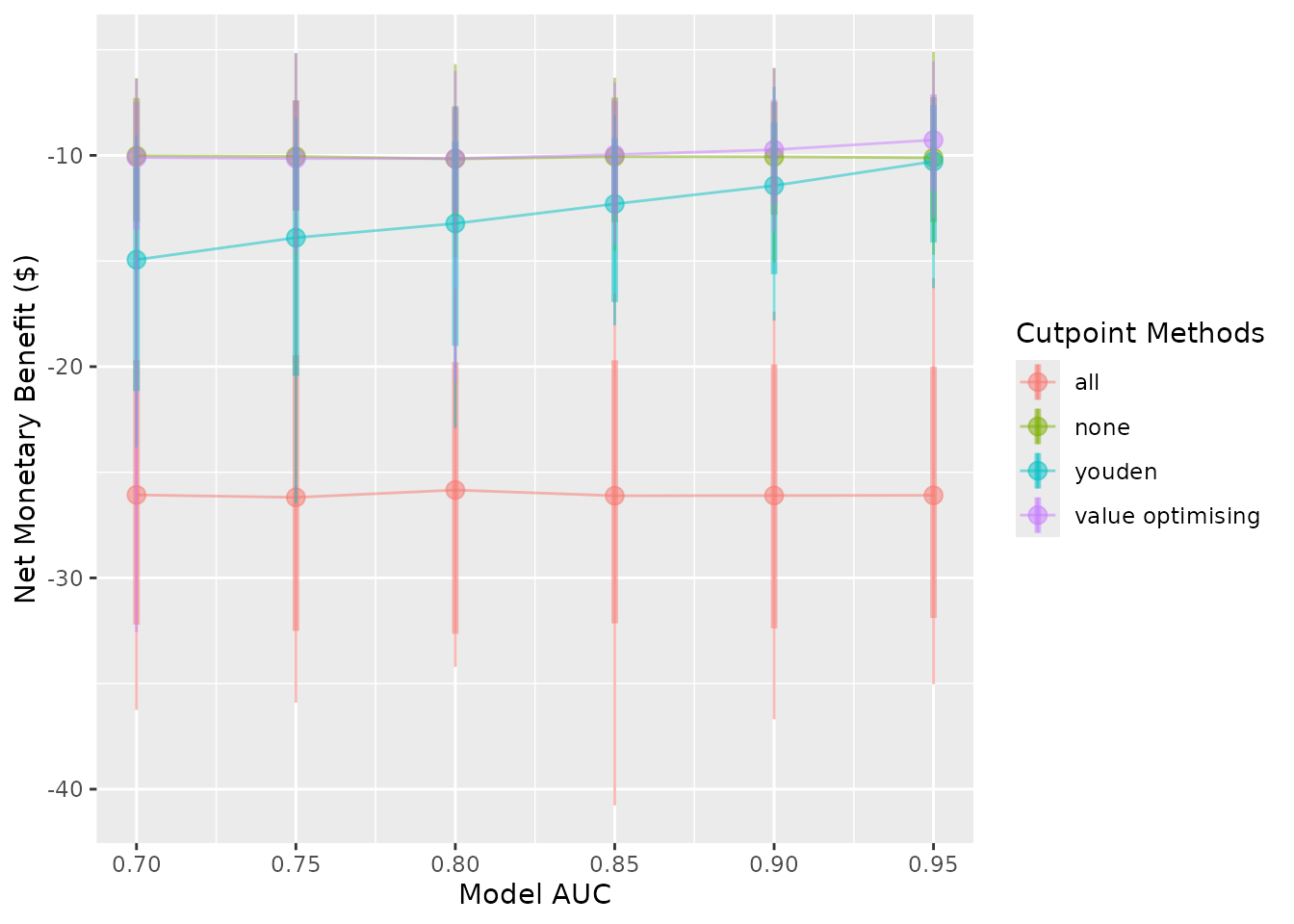

autoplot(sim_screen_obj, x_axis_var = "sim_auc", constants = list(event_rate = 0.2))
#> 
#> 
#> Varying simulation inputs, other than sim_auc, are being held constant:
#> event_rate: 0.2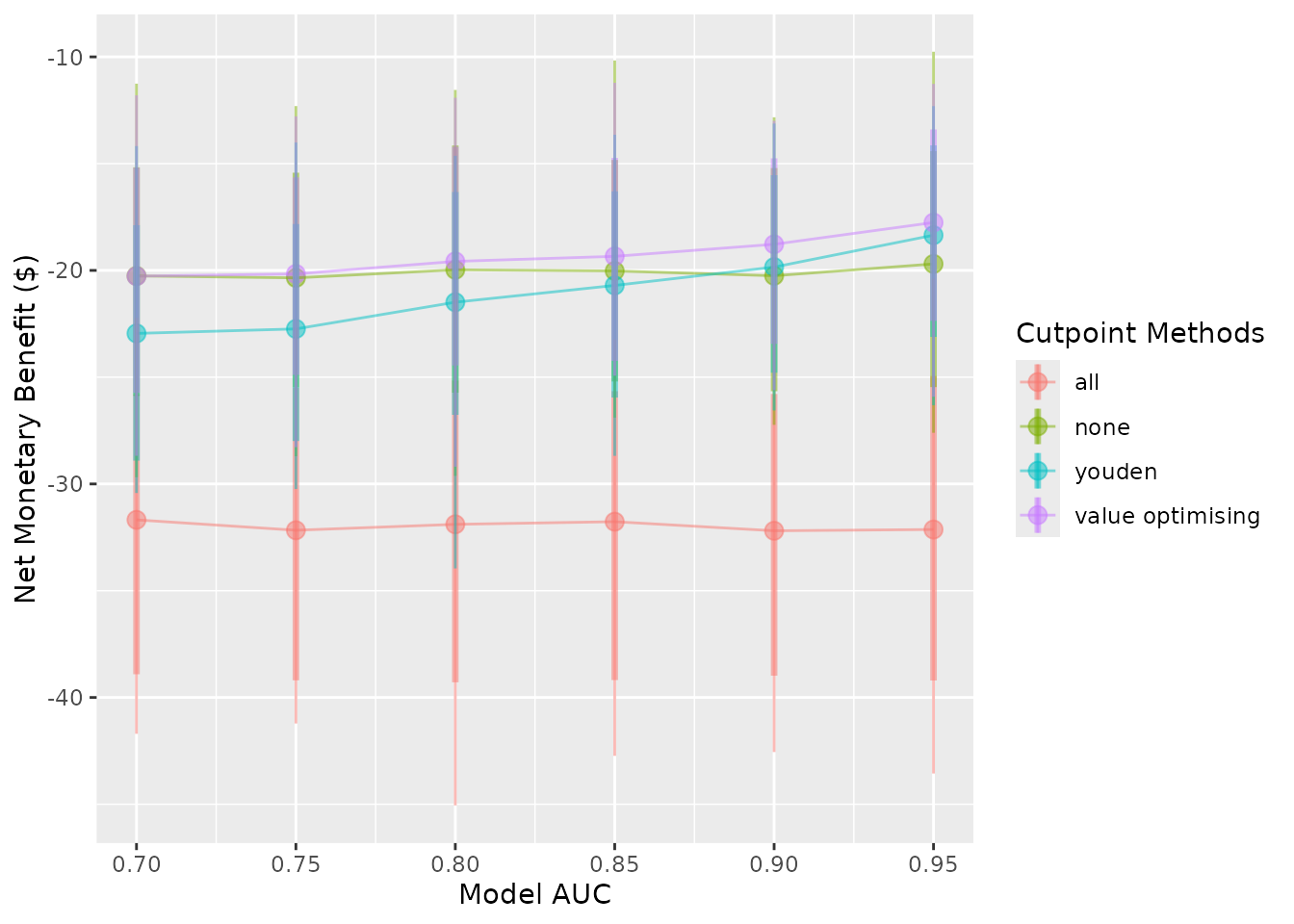

We see both a change to the plot as well as the message produced when the plot is made.

Choosing a y-axis variable

There are three options for the y-axis. The default is the NMB, but you can also visualise the Incremental Net Monetary Benefit (INB) and the selected cutpoints. These are controlled by the what argument, which can be any of c("nmb", "inb", "cutpoints"). If a vector is used, only the first value will be selected. If you choose to visualise the INB, you must list your chosen reference strategy for the calculation in the inb_ref_col. In this case, we use treat-all ("all").

autoplot(sim_screen_obj, what = "nmb")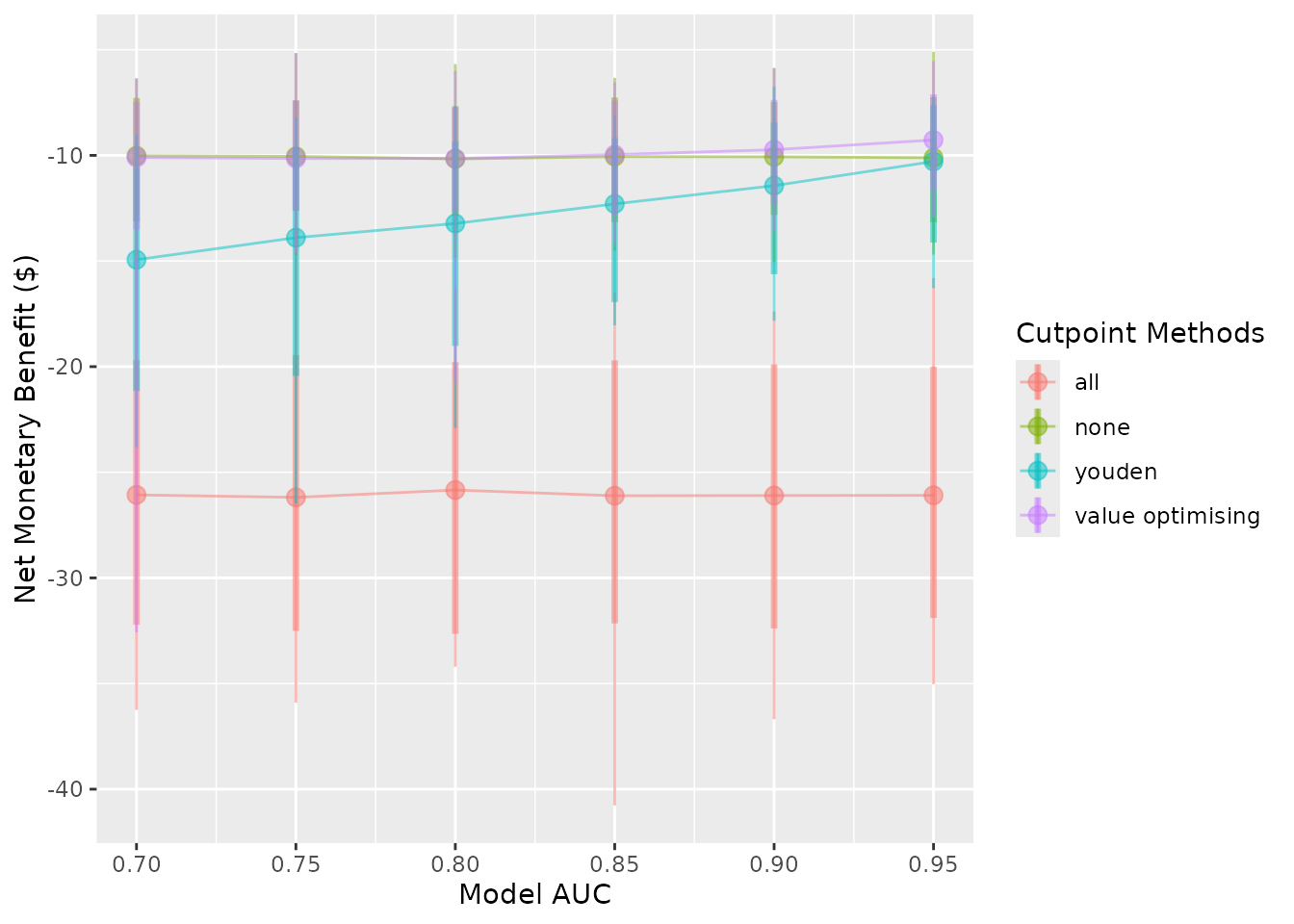

autoplot(sim_screen_obj, what = "inb", inb_ref_col = "all")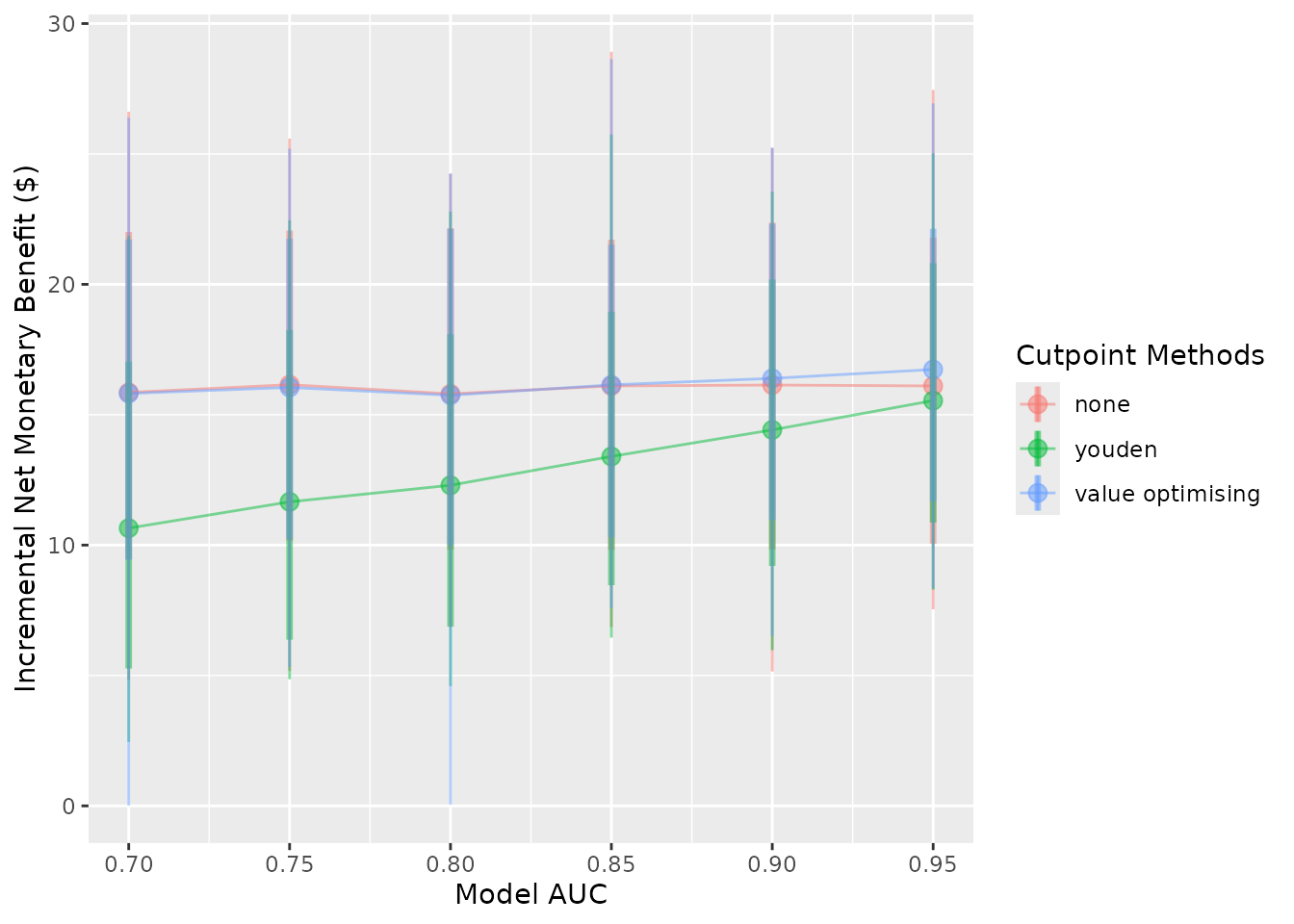

autoplot(sim_screen_obj, what = "cutpoints")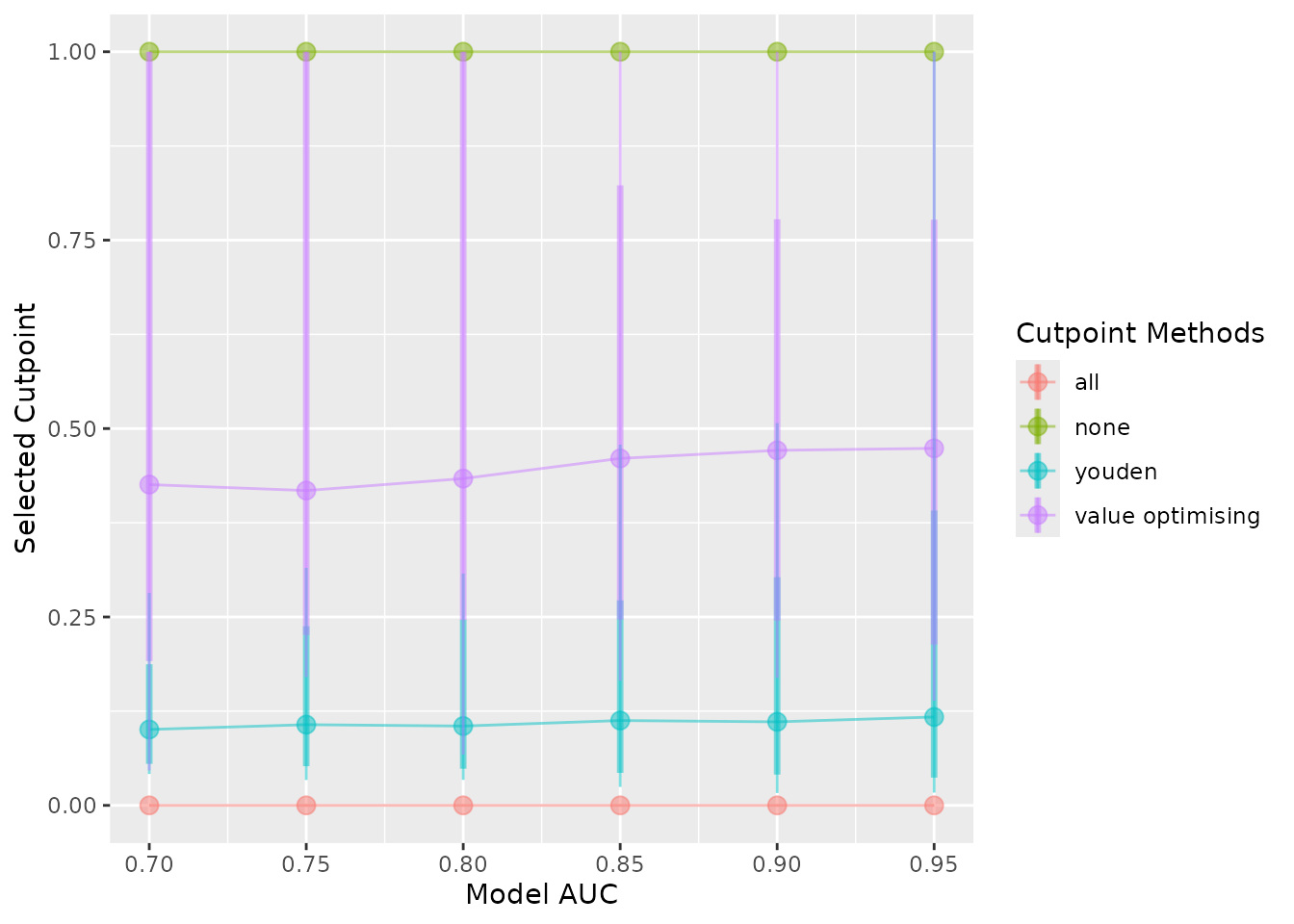

Selecting what to show on the plot

The plots show the median (the dot), the 95% confidence interval (thick vertical lines), the range (thin vertical lines), and the lines between the points by default. These can each be shown or hidden independently, and the width of the confidence interval can be controlled using the plot_conf_level argument.

autoplot(sim_screen_obj)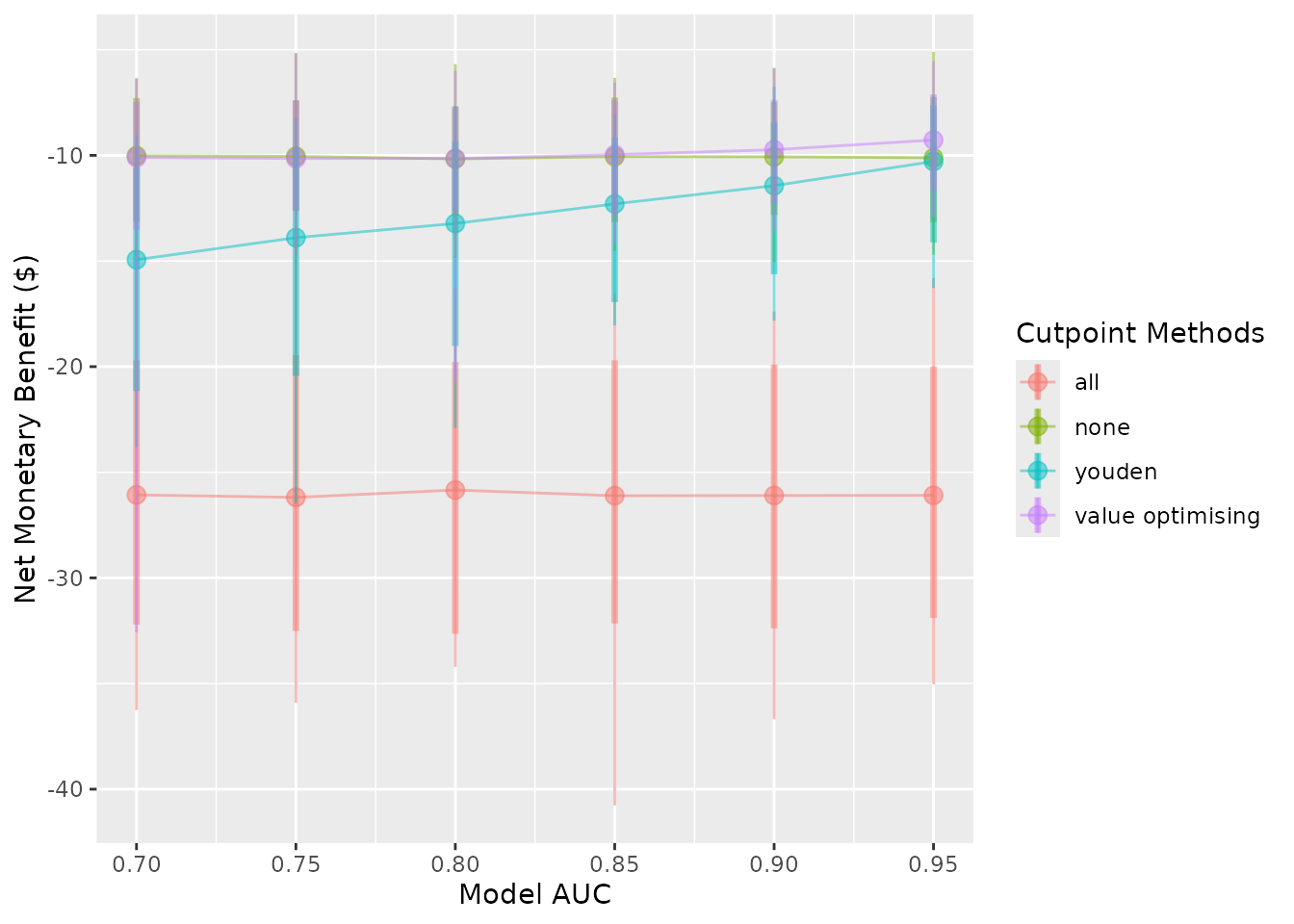

autoplot(sim_screen_obj, plot_range = FALSE)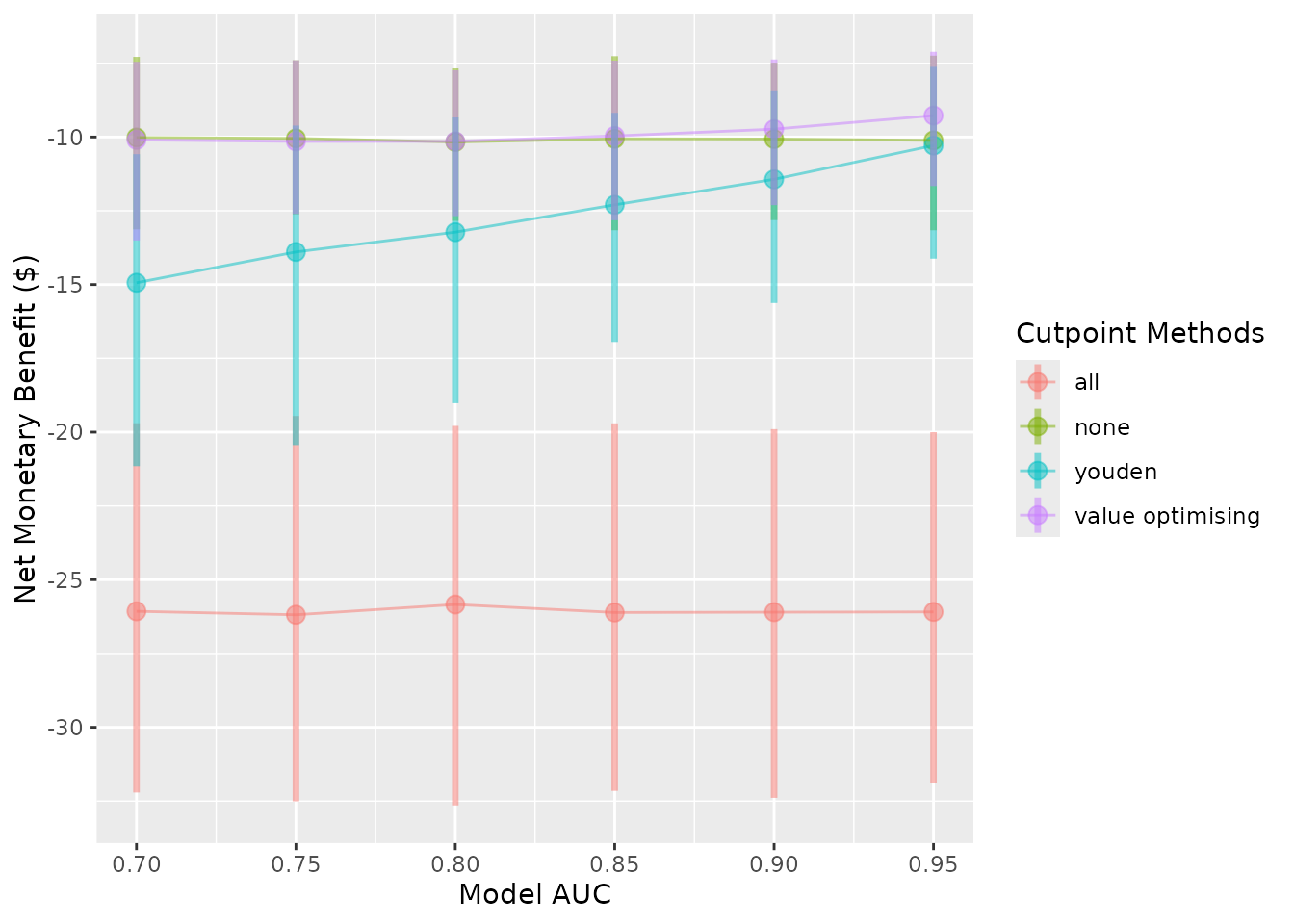

autoplot(sim_screen_obj, plot_conf_level = FALSE)

autoplot(sim_screen_obj, plot_conf_level = FALSE, plot_range = FALSE)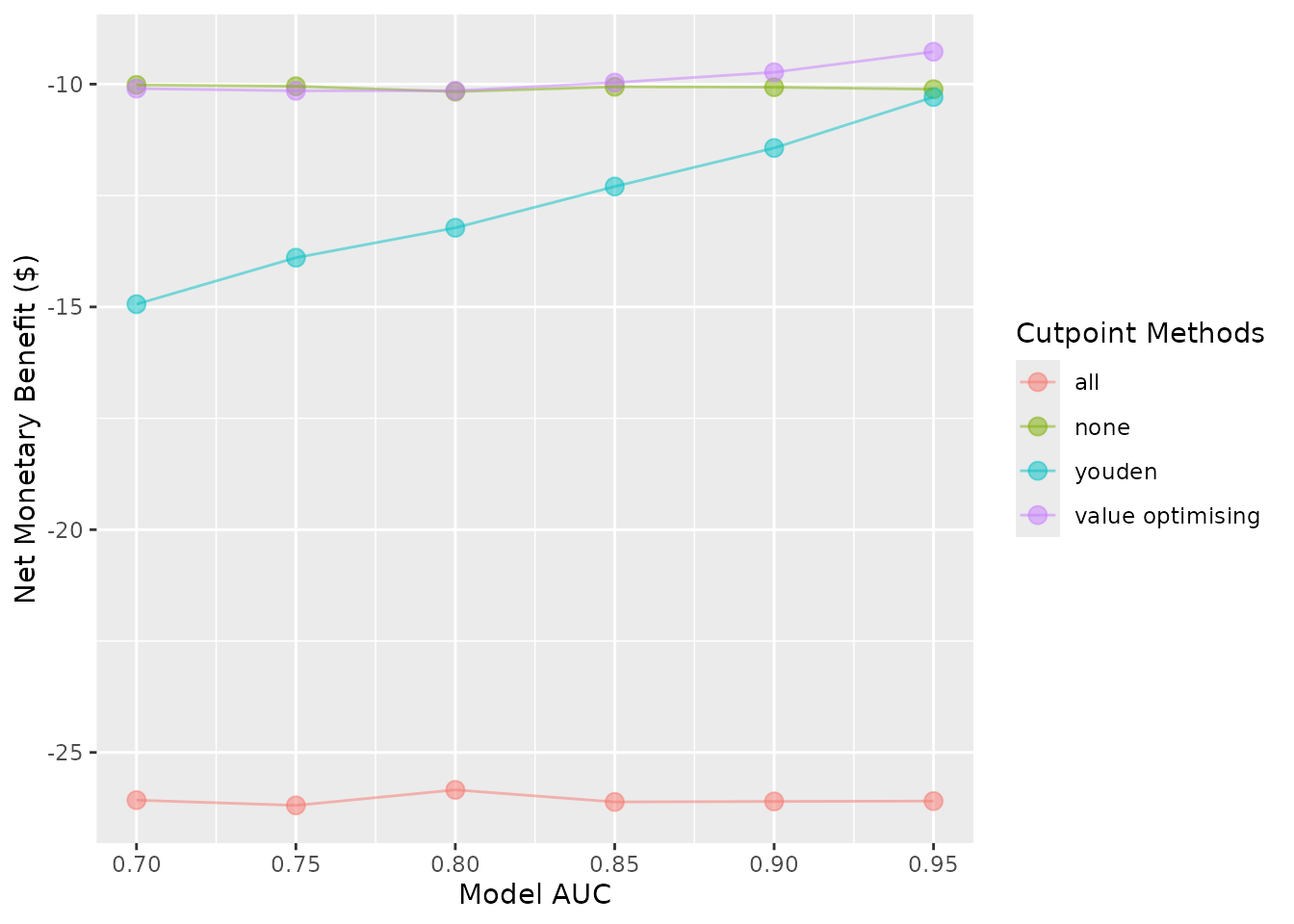

autoplot(sim_screen_obj, plot_conf_level = FALSE, plot_range = FALSE, plot_line = FALSE)

Other plot modifications

Currently, the lines and dots overlap. We can use dodge_width to apply a horizontal dodge for all layers.

autoplot(sim_screen_obj, dodge_width = 0.01)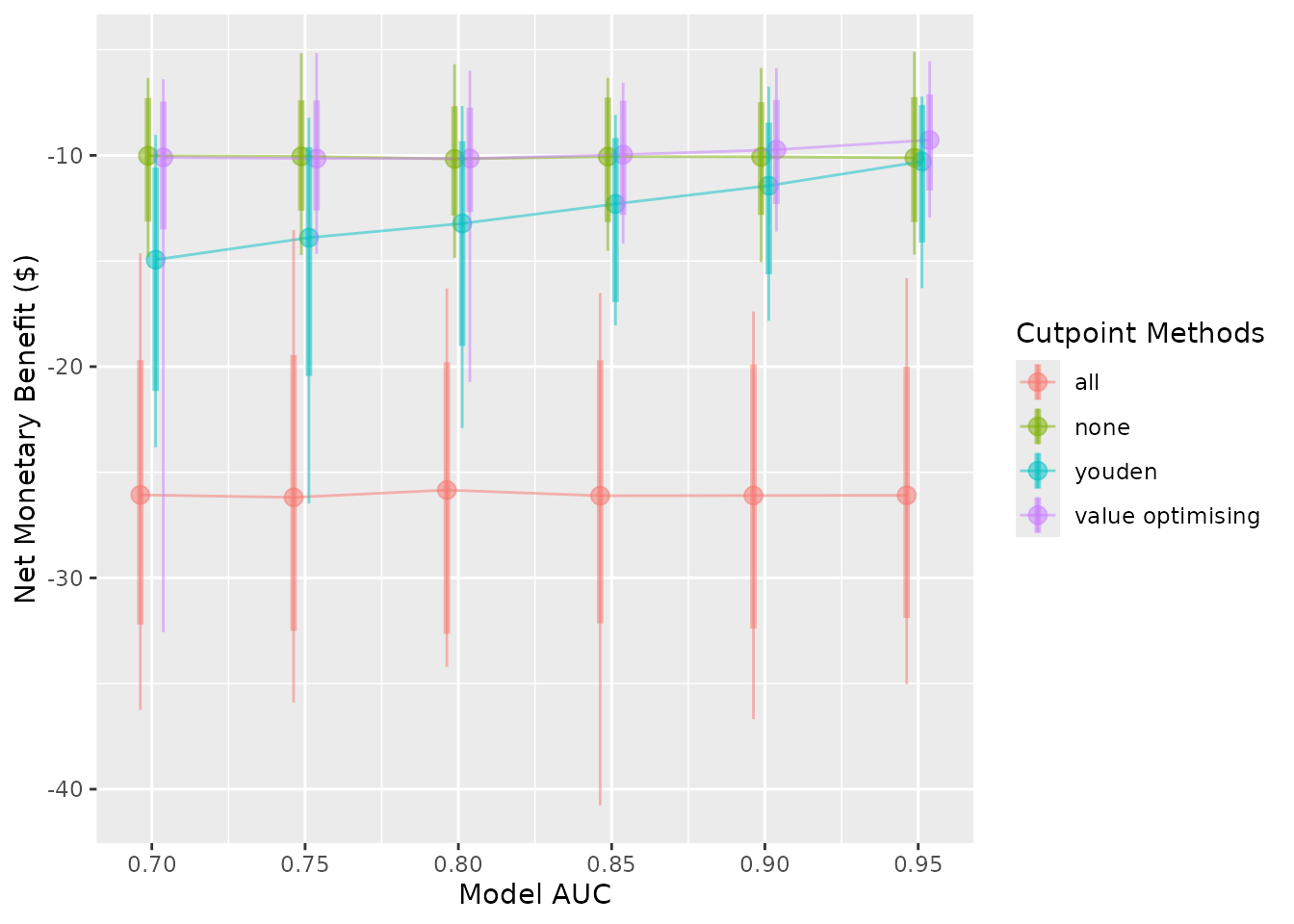

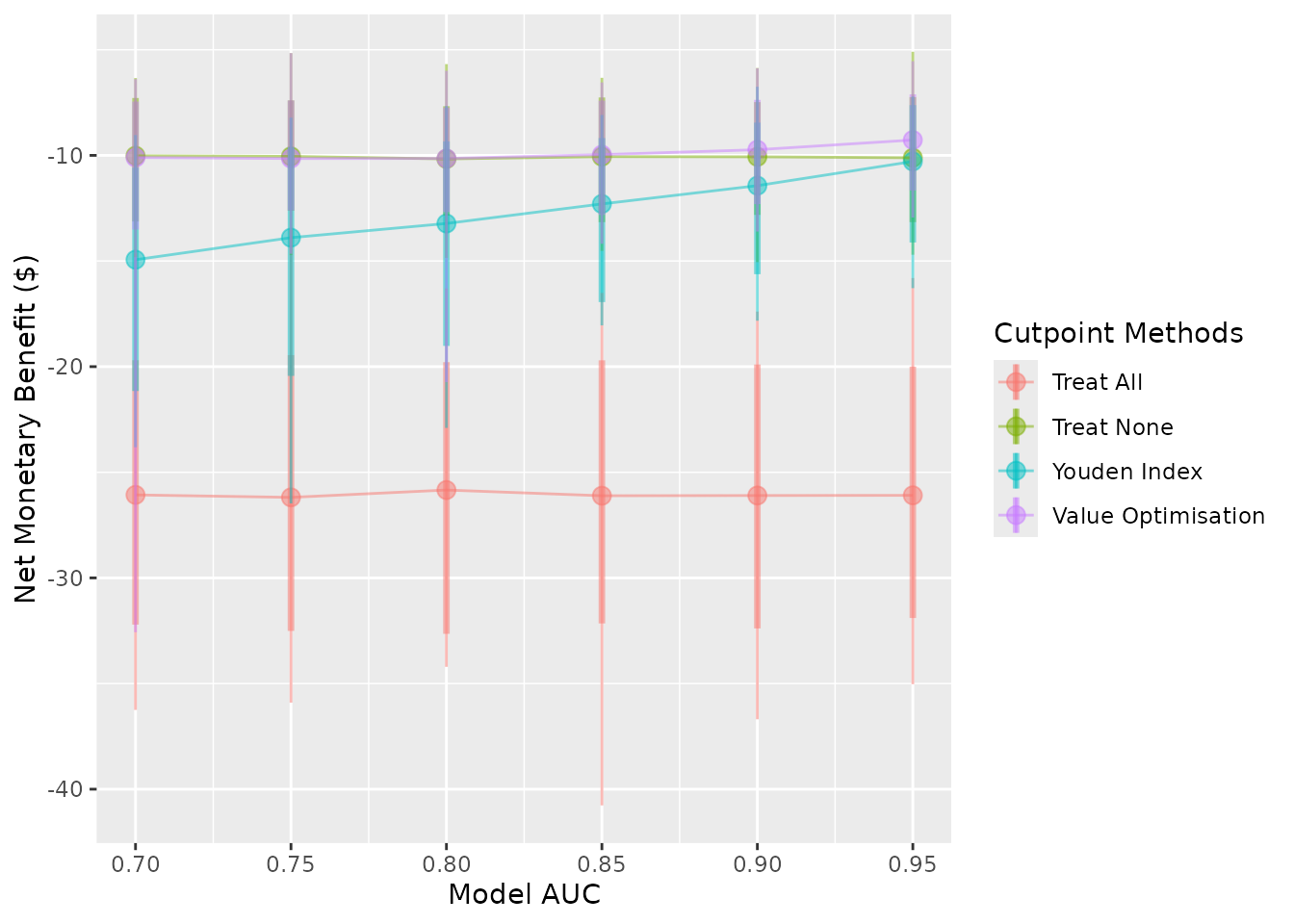
The cutpoint methods can be renamed or removed. To rename them, pass a named vector to the rename_vector argument. The names of the vector are the new names and the values are the names you wish to replace.

autoplot(
  sim_screen_obj,
  rename_vector = c("Treat All" = "all", 
                    "Treat None" = "none",
                    "Youden Index" = "youden", 
                    "Value Optimisation" = "value_optimising")
)

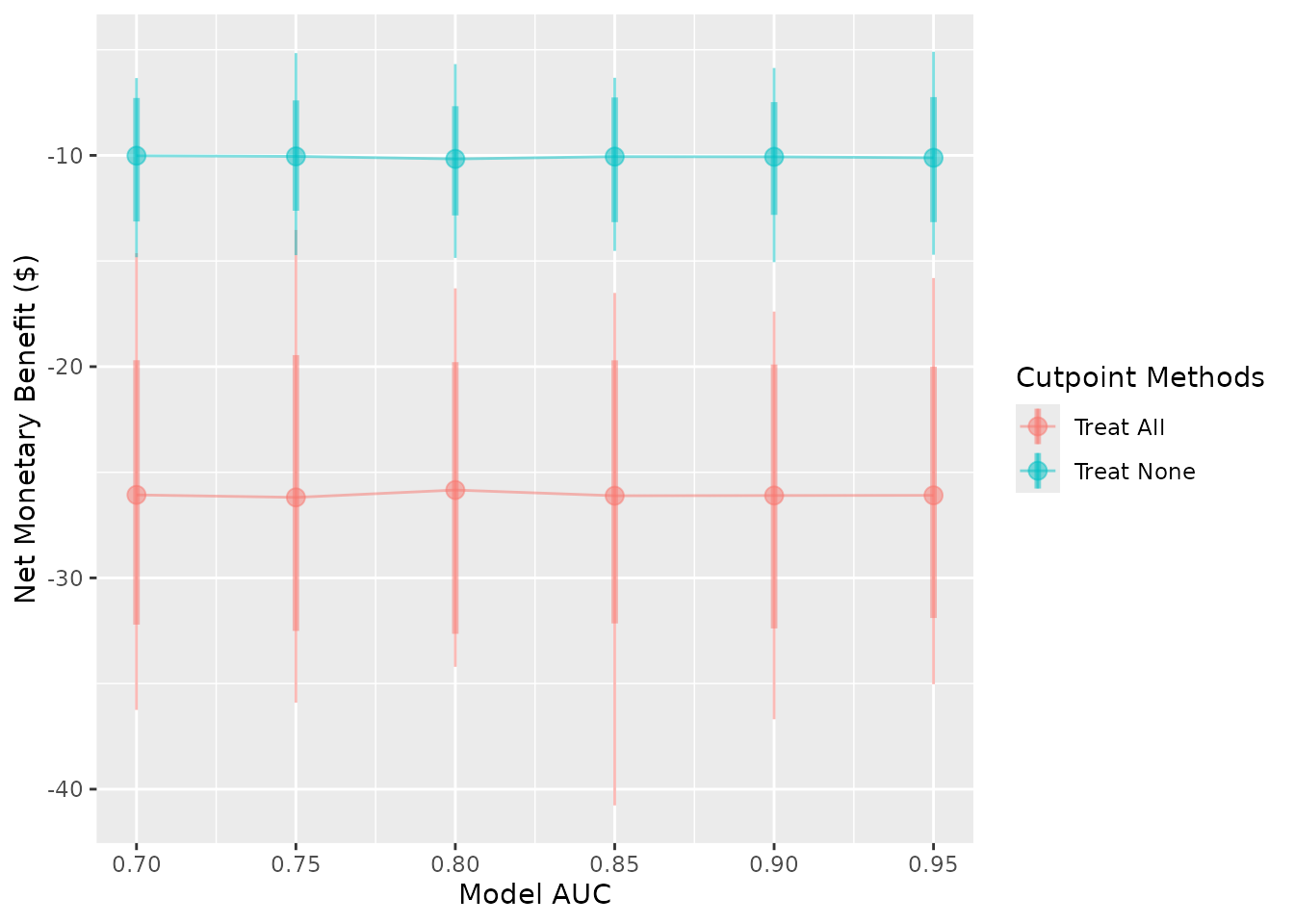
You can reorder the methods by passing the order as the methods_order argument. Also note that this will remove all methods which aren’t included, and it will factor the names AFTER it has renamed them. So, if you are both renaming and re-ordering, you must provide the updated names when you order them:

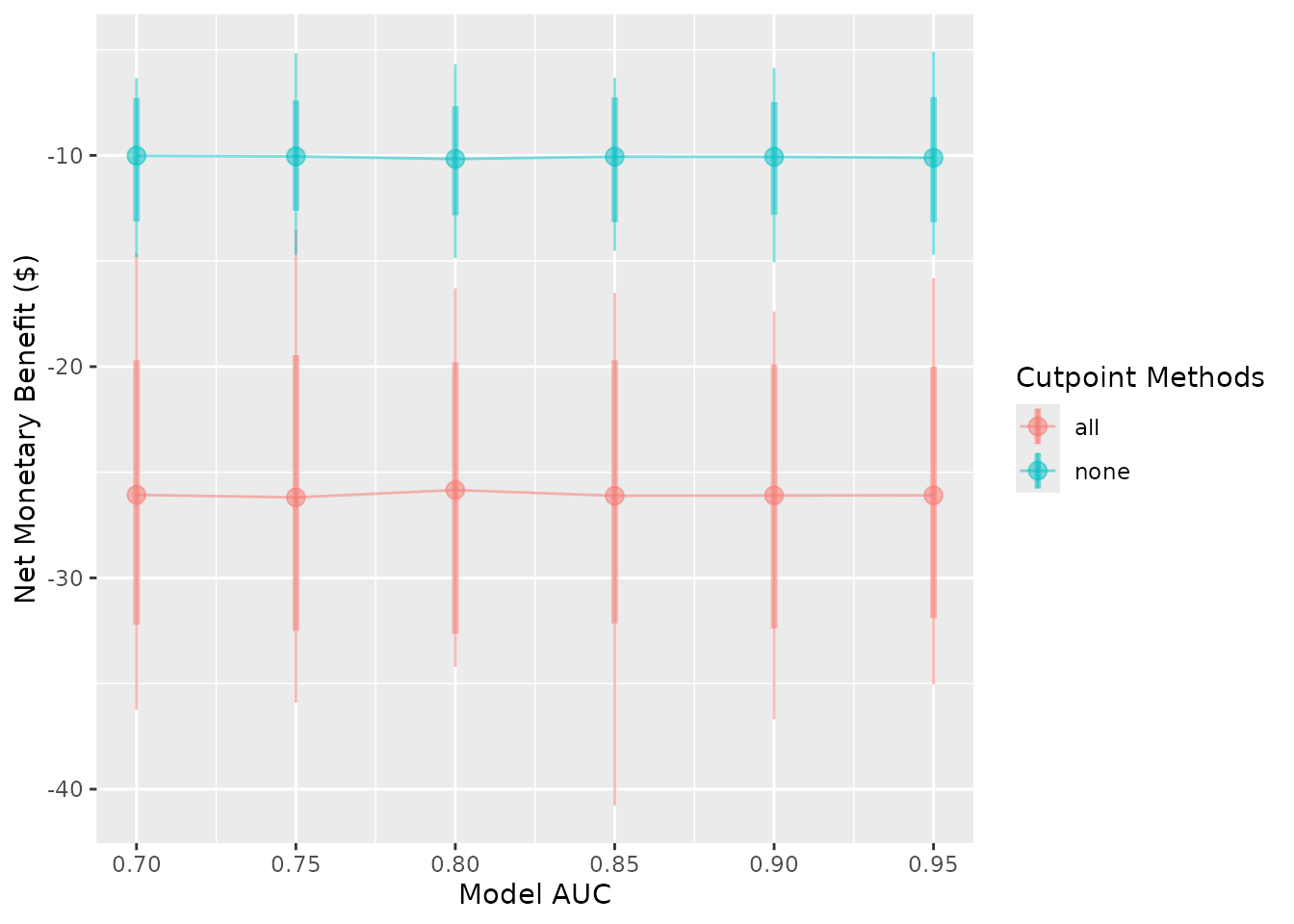
autoplot(sim_screen_obj, methods_order = c("all", "none"))

autoplot(
  sim_screen_obj,
  # Assign new names to the two methods of interest
  rename_vector = c("Treat All" = "all", "Treat None" = "none"), 
  
  # Call the methods by their new names
  methods_order = c("Treat All", "Treat None") 
)

The transparency of all layers can be controlled with plot_alpha.

autoplot(sim_screen_obj, plot_alpha = 0.2)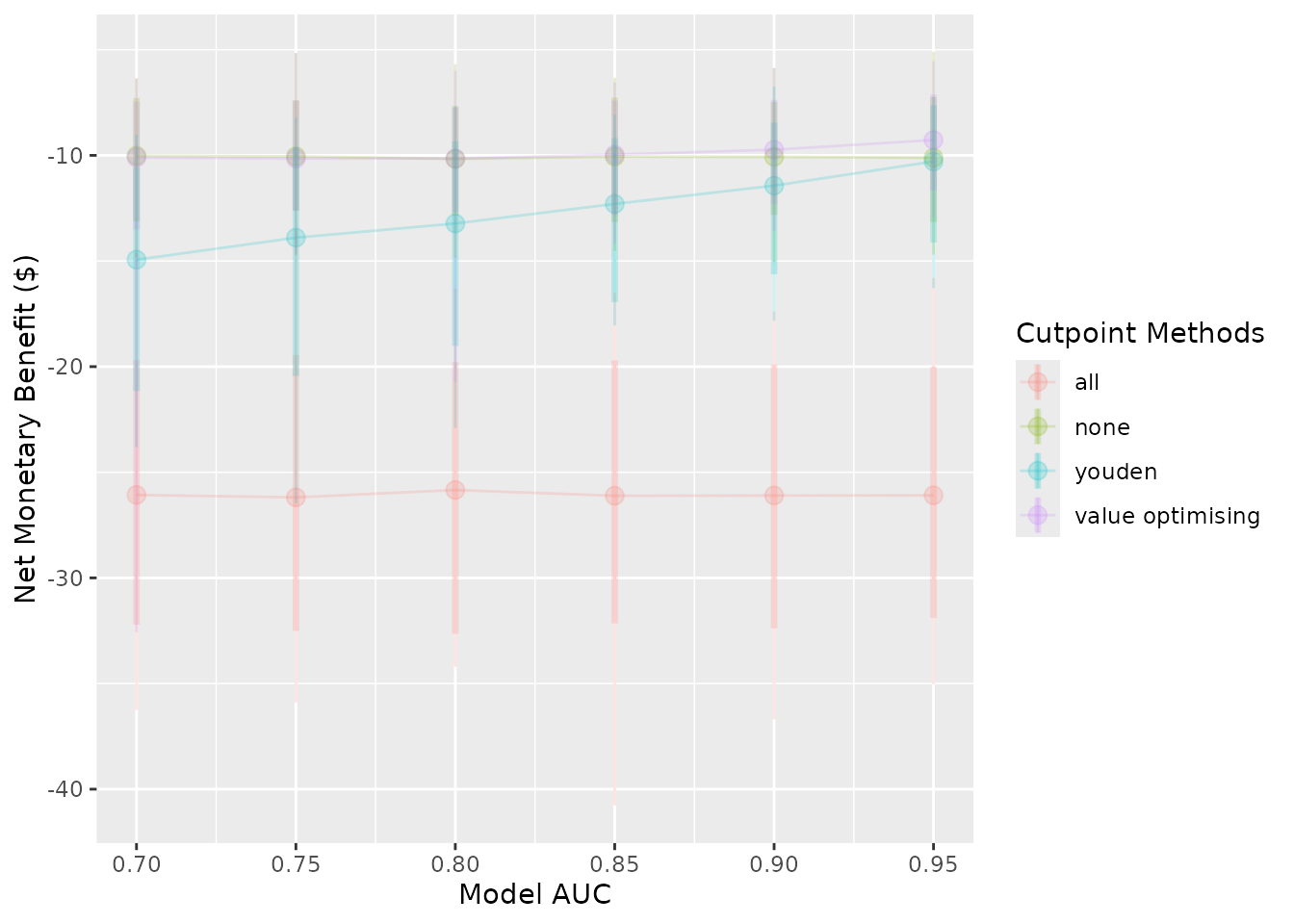

autoplot(sim_screen_obj, plot_alpha = 1)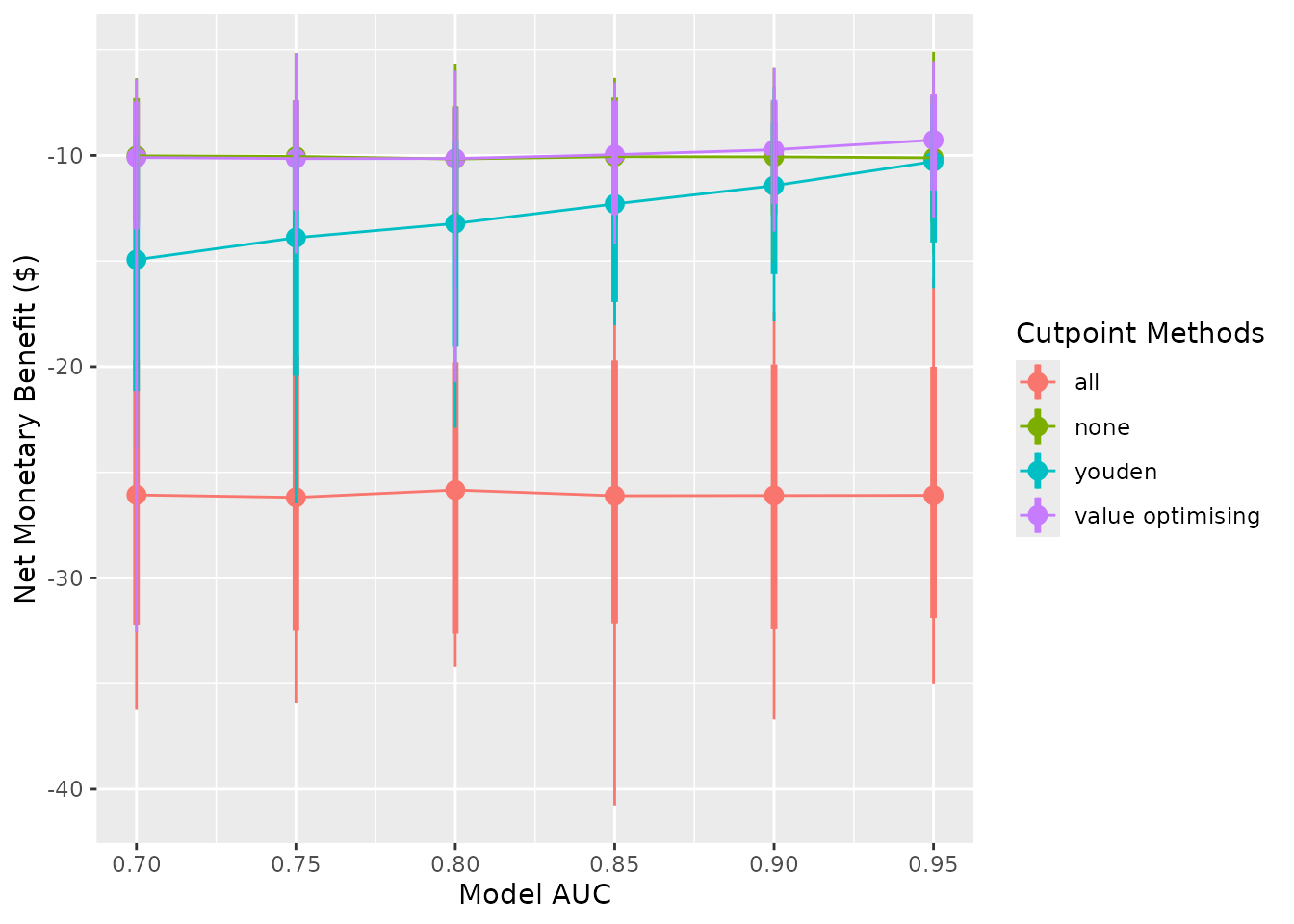

Plotting the results from do_nmb_sim()

Many of the same arguments that we used above can be used with the object returned from do_nmb_sim()

do_nmb_sim_obj <- do_nmb_sim(
  n_sims = 500,
  n_valid = 10000,
  sim_auc = 0.7,
  event_rate = 0.1,
  fx_nmb_training = get_nmb_sampler_training,
  fx_nmb_evaluation = get_nmb_sampler_evaluation,
  cutpoint_methods = c("all", "none", "youden", "value_optimising")
)

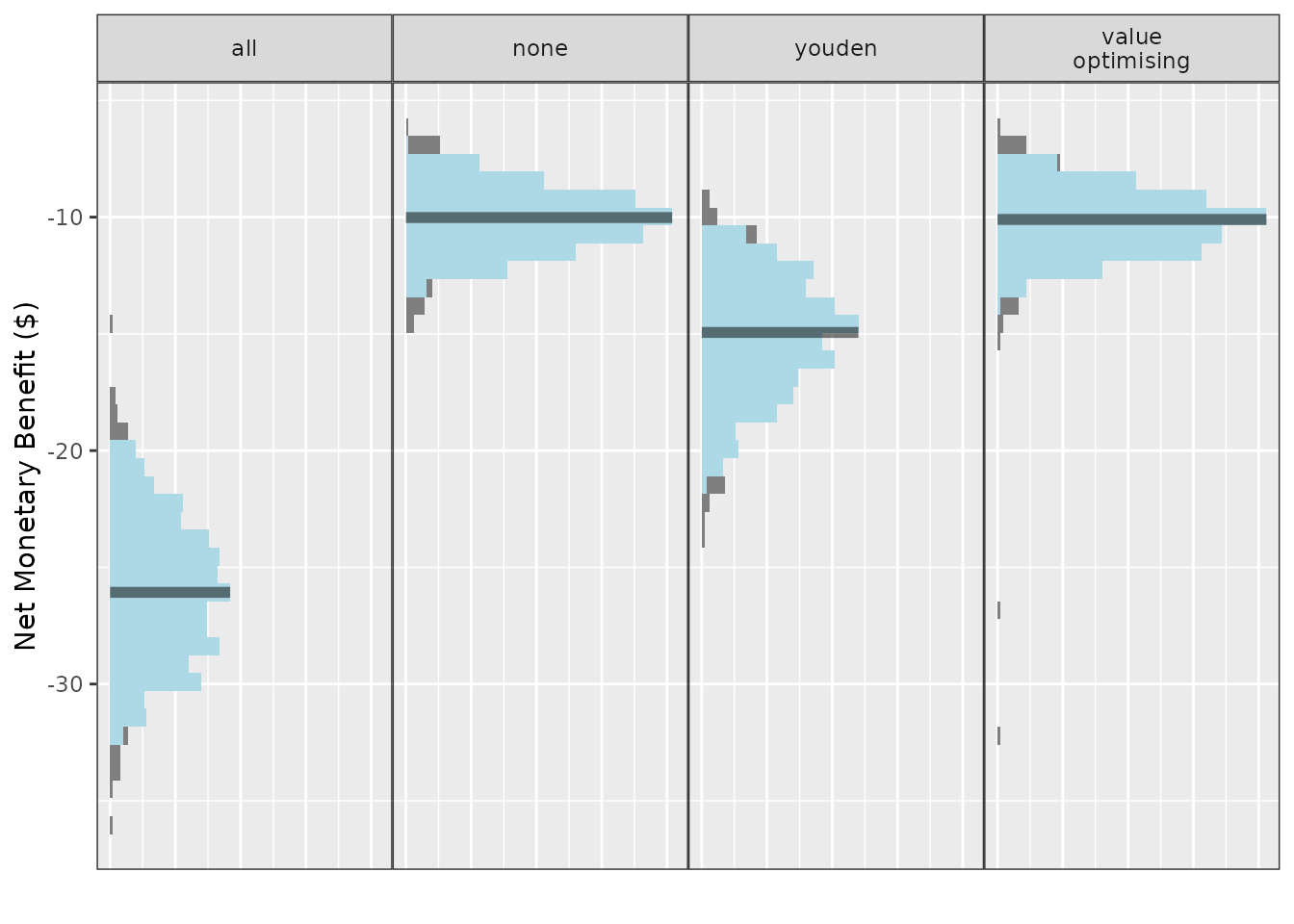
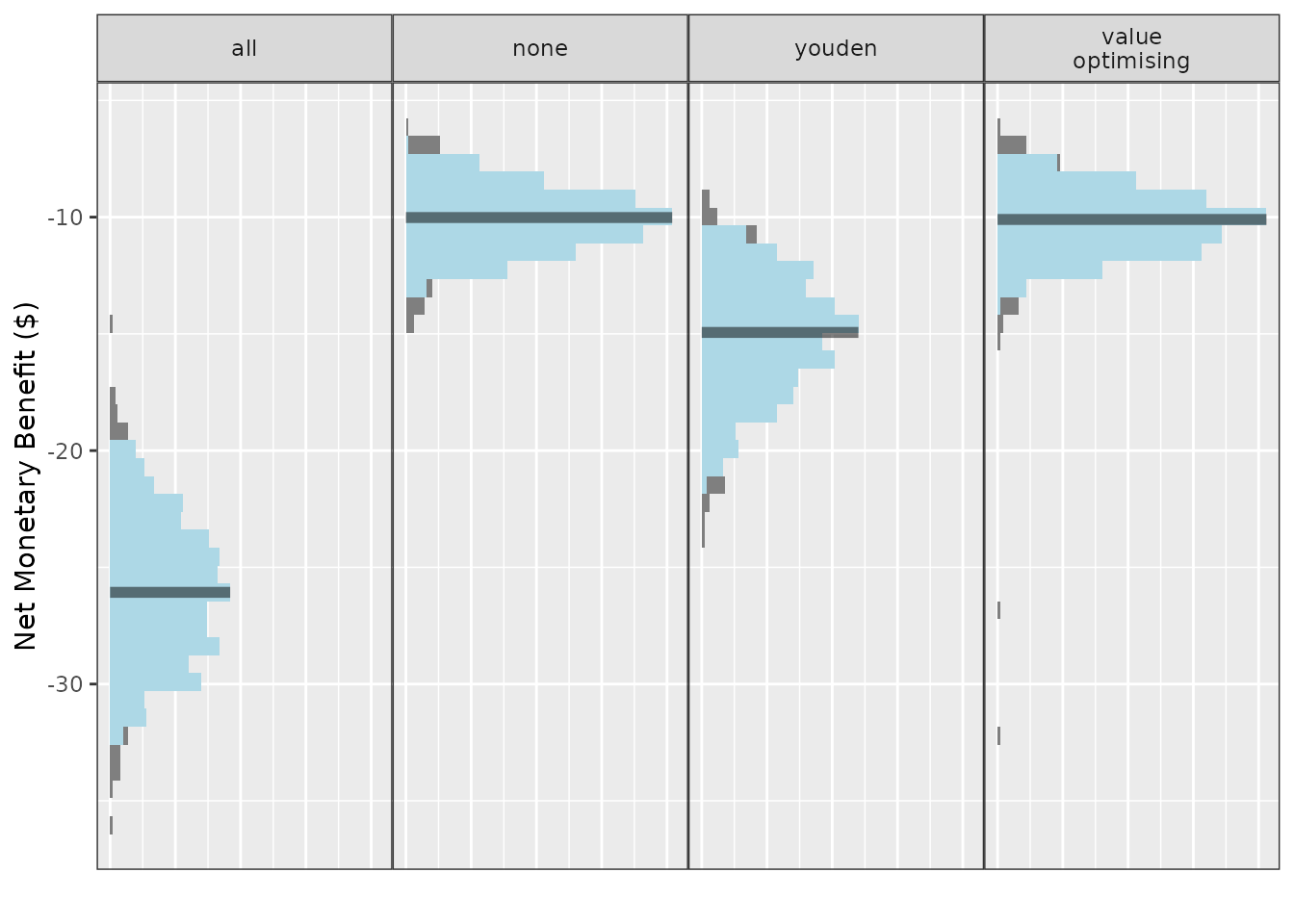
autoplot()

The plots here show the results of a single simulation and compare the available cutpoints.

autoplot(do_nmb_sim_obj) + theme_sim()

The y-axis variable and names and orders of methods can be controlled in the same way as previously:

autoplot(do_nmb_sim_obj, what = "nmb") + theme_sim()

autoplot(
  do_nmb_sim_obj,
  what = "inb",
  inb_ref_col = "all",
  rename_vector = c(
    "Value-Optimising" = "value_optimising",
    "Treat-None" = "none",
    "Youden Index" = "youden"
  )
) + theme_sim()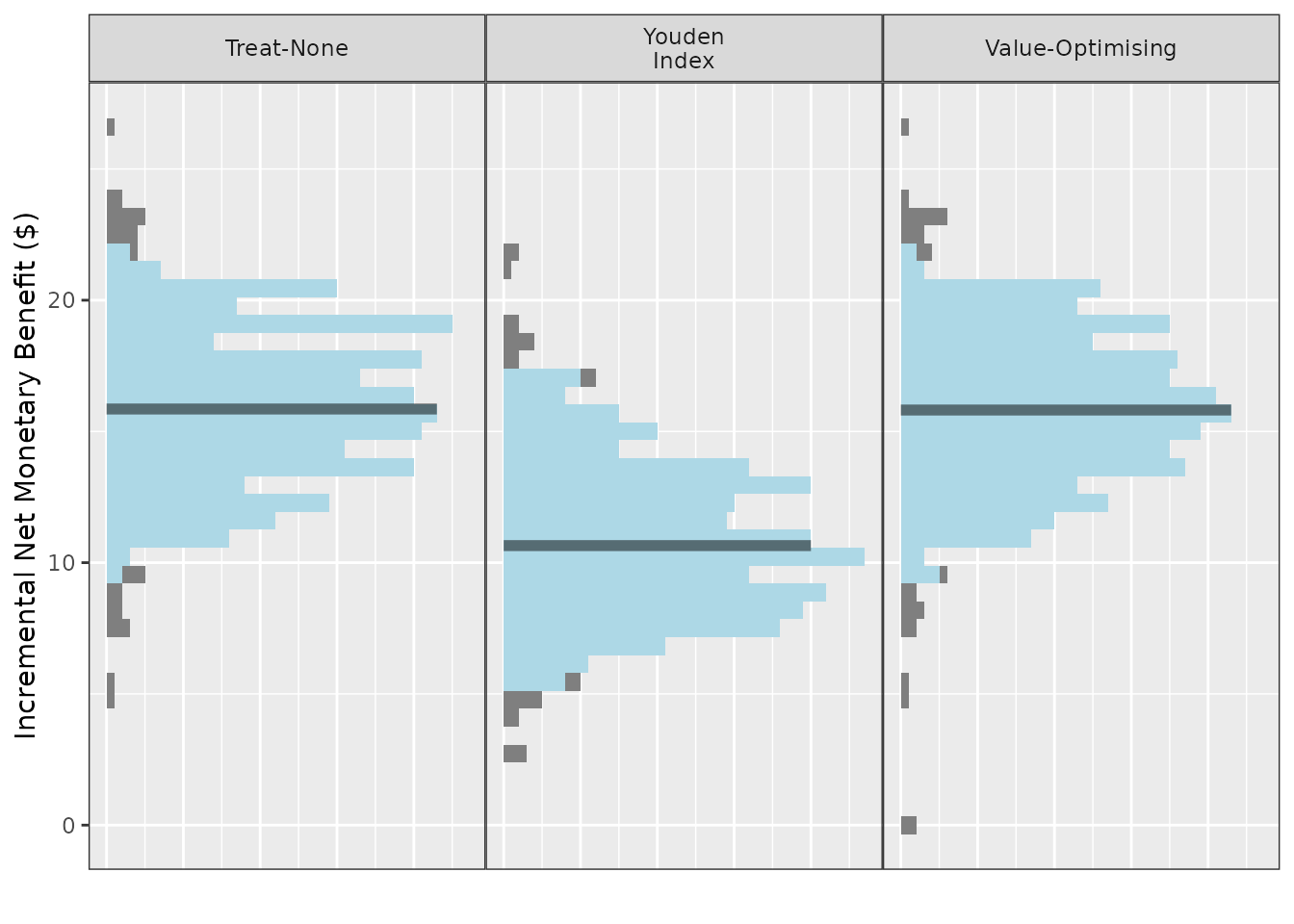

autoplot(
  do_nmb_sim_obj,
  what = "cutpoints",
  methods_order = c("all", "none", "youden", "value optimising")
) + theme_sim()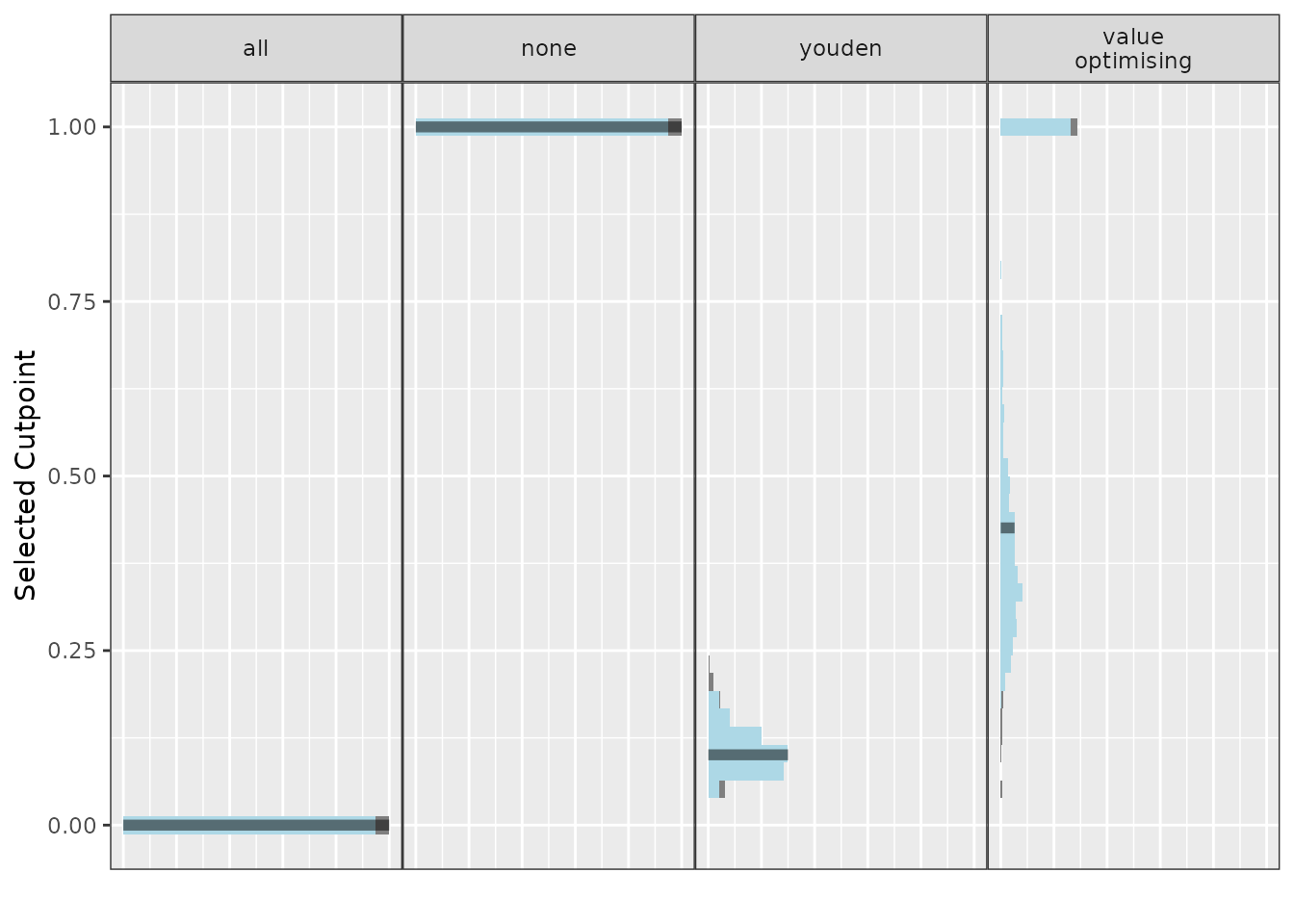

These plots display the median as the solid bar, the grey part of the distributions are the outer 5% of the simulated values and the light blue region is the 95% CI. For the methods that select thresholds based on the values in the 2x2 table, including the value-optimising thresholds, this may look a little strange as the cutpoints are highly variable. This can be stabilised with more simulations. The fill colours of the histogram are controlled with fill_cols and the line for the median is controlled with median_line_col. The thickness of the median line is controlled with median_line_size and its transparency with median_line_alpha.

autoplot(
  do_nmb_sim_obj,
  fill_cols = c("red", "blue"),
  median_line_col = "yellow",
  median_line_alpha = 1,
  median_line_size = 0.9
) + theme_sim()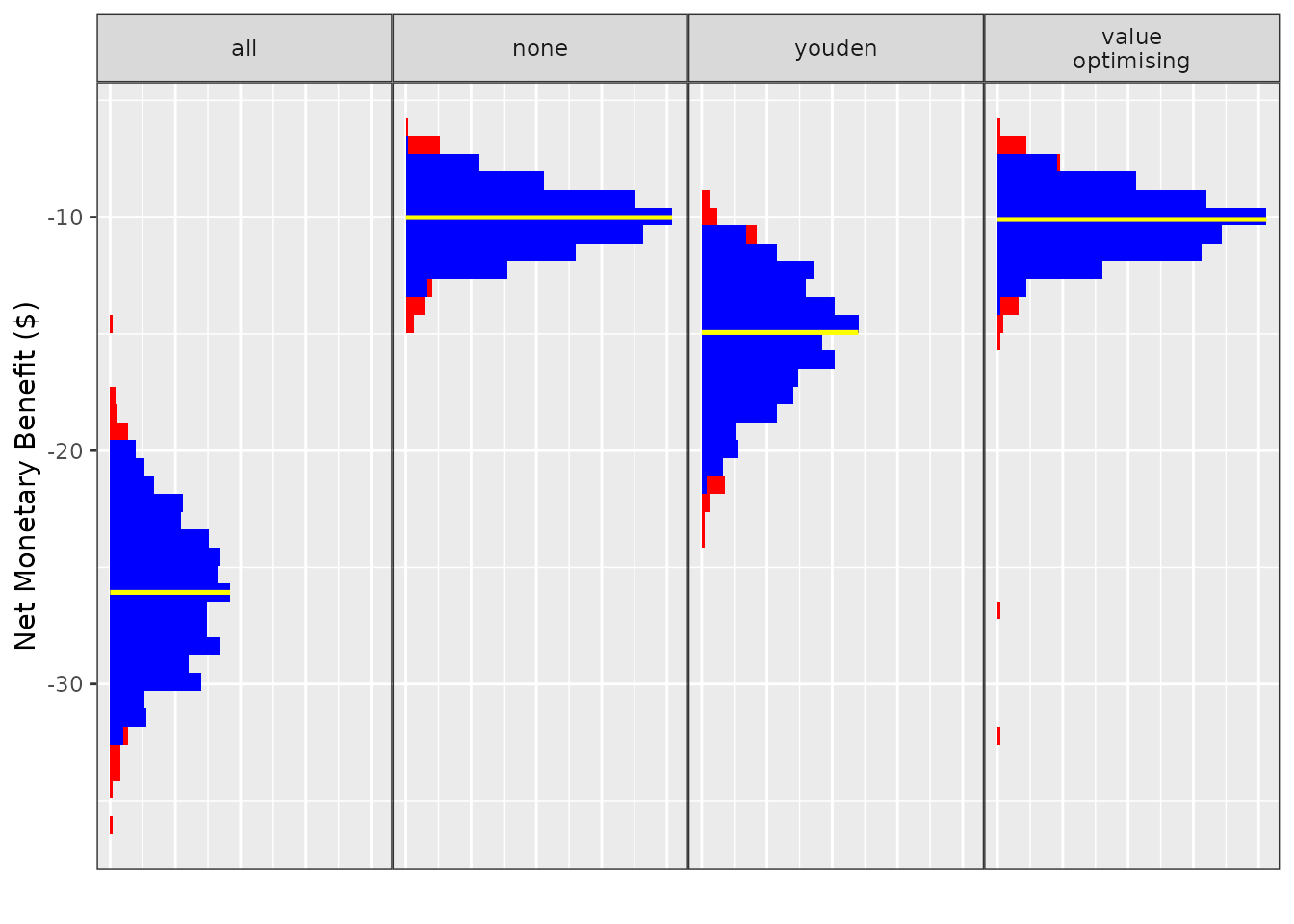

The n_bins argument controls the number of bins used for the histograms and the label_wrap_width is the number of characters above which to start a new line for the facet labels. This can be handy when using detailed names for the methods when the font of the label is relatively large compared to the plot, though a space is needed to determine where to split the label. The width of the confidence intervals can also be controlled by the conf.level argument in this autoplot() call.

autoplot(
  do_nmb_sim_obj,
  n_bins = 15,
  rename_vector = c(
    "Value- Optimising" = "value_optimising",
    "Treat- None" = "none",
    "Treat- All" = "all",
    "Youden Index" = "youden"
  ),
  label_wrap_width = 5,
  conf.level = 0.8
) + theme_sim()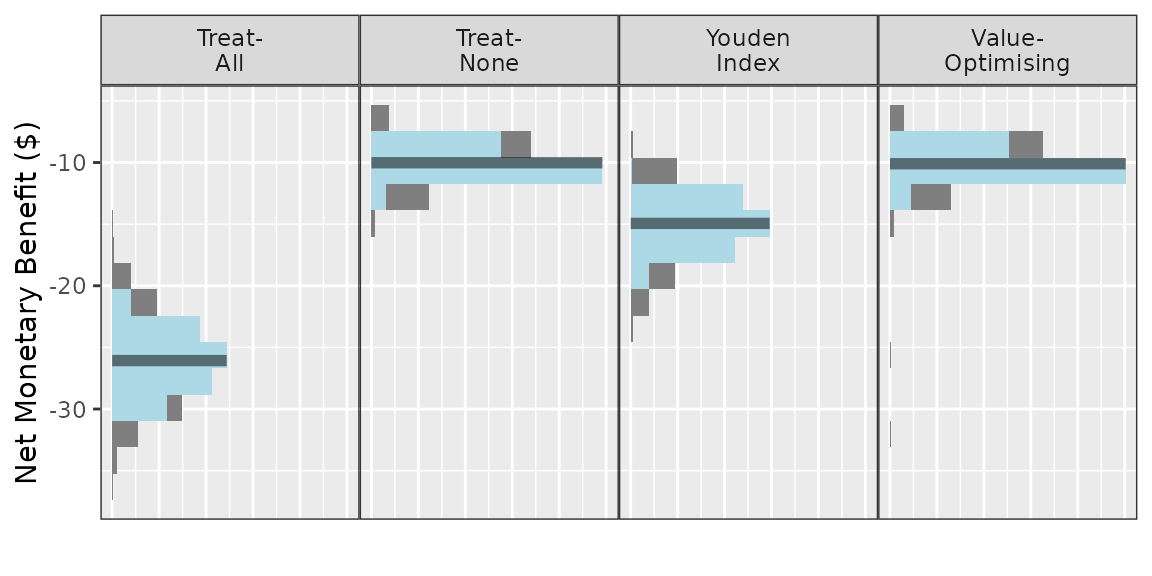

ce_plot()

A cost-effectiveness plot may be useful to decision-makers deciding between competing alternatives as it shows both the incremental healthcare costs associated with the change as well as the incremental improvement in patient benefit (QALYs). For a detailed explanation on how to interpret cost-effectiveness plots, see (Fenwick et al. 2006).

For these plots, a reference group must be specified with ref_col. In this example, the reference group is to treat none.

ce_plot(do_nmb_sim_obj, ref_col = "none")

Similarly to autoplot(), the methods can be selected and renamed using methods_order and rename_vector. The diagonal line is the cost-effectiveness plane and this is based on the willingness to pay. In this example, it was $28033 and is stored within the predictNMBsim object via the fx_nmb_evaluation function that was originally used. Simulations underneath the cost-effectiveness plane are deemed cost-effective.

attr(do_nmb_sim_obj$meta_data$fx_nmb_evaluation, "wtp")
#> [1] 28033

The WTP can be adjusted using the WTP argument but it is not advisable to use a different value to what was used in the initial simulations because the plotted WTP will be different to the simulation objects. If a different WTP value should be investigated, it is advisable to re-run the simulations again as do_nmb_sim objects.

ce_plot(do_nmb_sim_obj, ref_col = "none", wtp = 100000)
#> wtp is stored in predictNMBsim object (wtp = 28033)
#> 
#> but has also been specified (wtp = 1e+05)
#> 
#> Using a different WTP for evaluating the simulations (NMB) and within the cost-effectiveness plot may lead to misinterpretation!

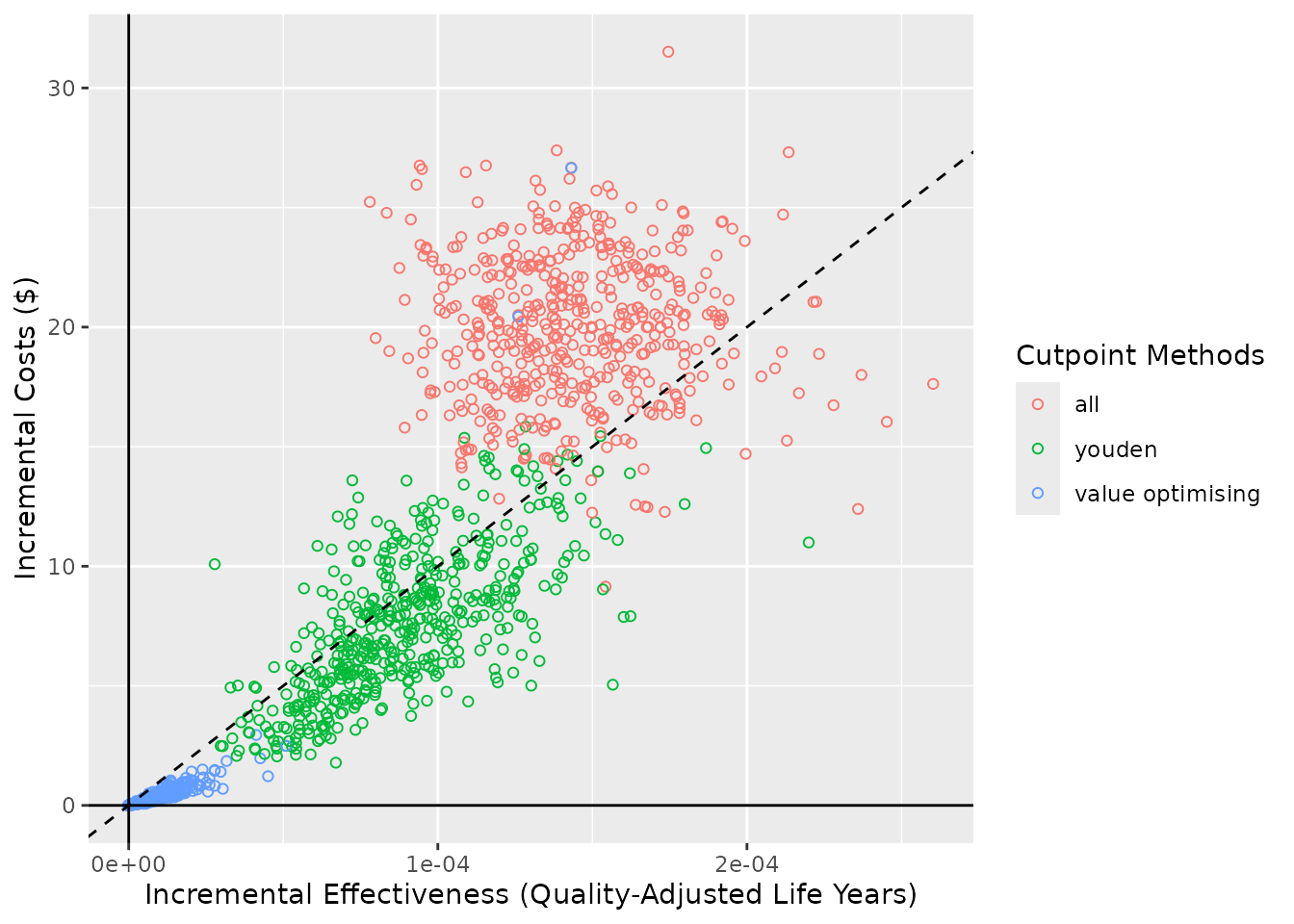
The line can be removed by using show_wtp = FALSE.

ce_plot(do_nmb_sim_obj, ref_col = "none", show_wtp = FALSE)

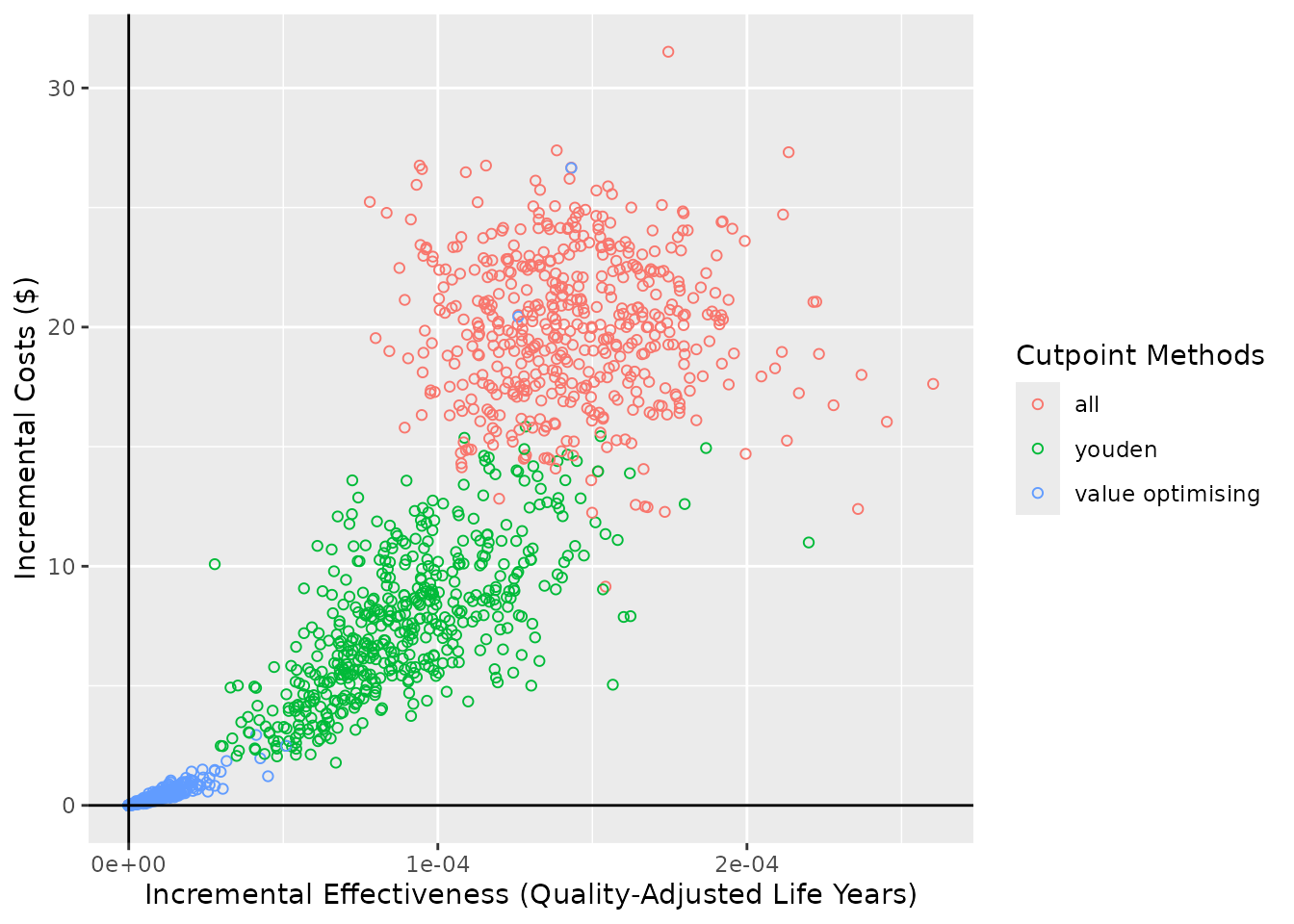
The shape argument controls the shape aesthetic in geom_point(). It can also be mapped to whether the point is “cost-effective” (falls beneath the cost-effectiveness plane/WTP line) or the cutpoint “method”, and the proportion of cost-effective simulations can be added to the methods section of the legend if add_prop_ce = TRUE. For the sake of demonstration, we’ll change the WTP line for the “cost-effective” shape input.

ce_plot(do_nmb_sim_obj, ref_col = "none", shape = 15, add_prop_ce = TRUE)

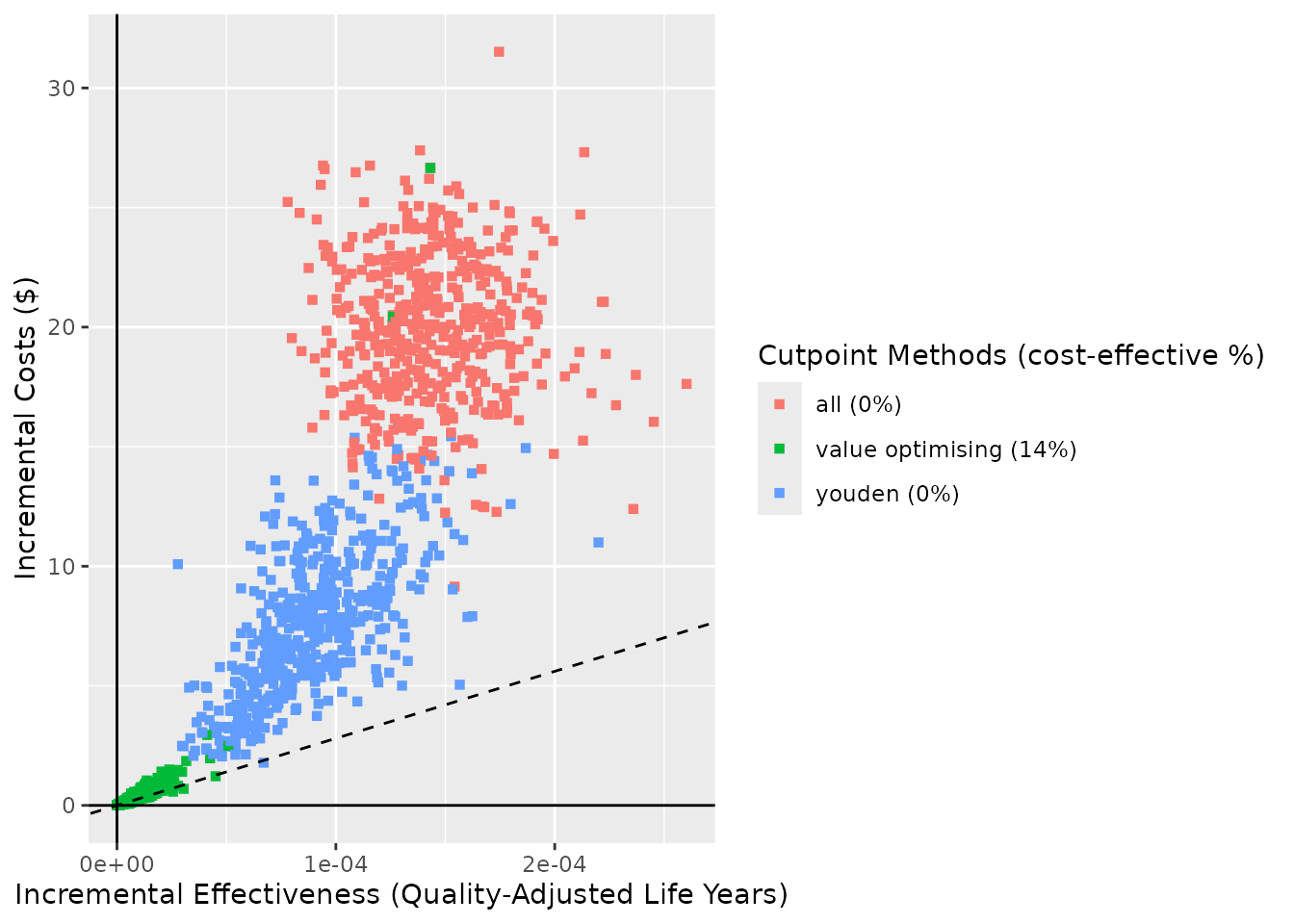
ce_plot(do_nmb_sim_obj, ref_col = "none", shape = "square", add_prop_ce = TRUE)

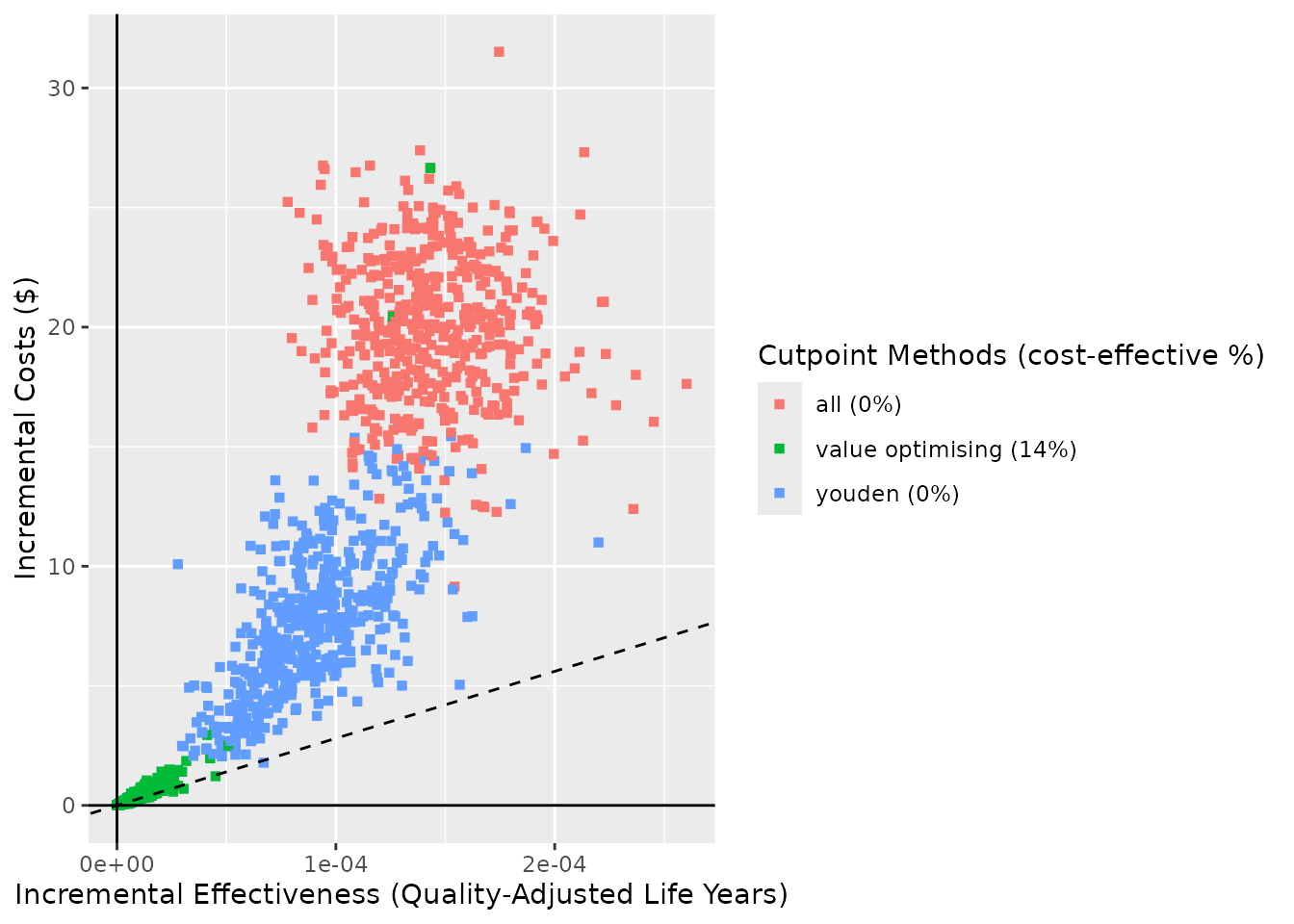
ce_plot(do_nmb_sim_obj, ref_col = "none", shape = "cost-effective", wtp = 80000, add_prop_ce = TRUE)
#> wtp is stored in predictNMBsim object (wtp = 28033)
#> 
#> but has also been specified (wtp = 80000)
#> 
#> Using a different WTP for evaluating the simulations (NMB) and within the cost-effectiveness plot may lead to misinterpretation!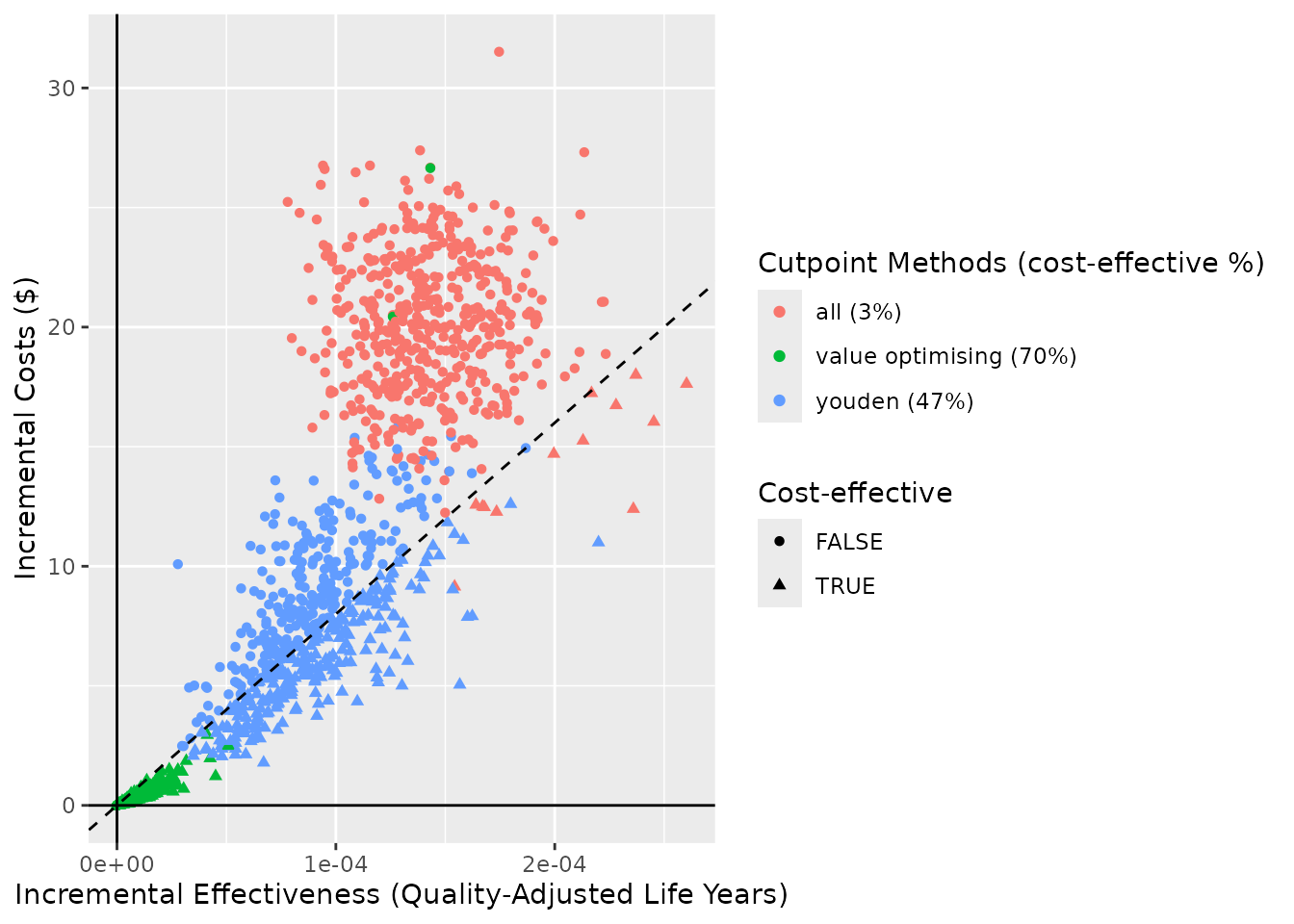

ce_plot(do_nmb_sim_obj, ref_col = "none", shape = "method", add_prop_ce = TRUE)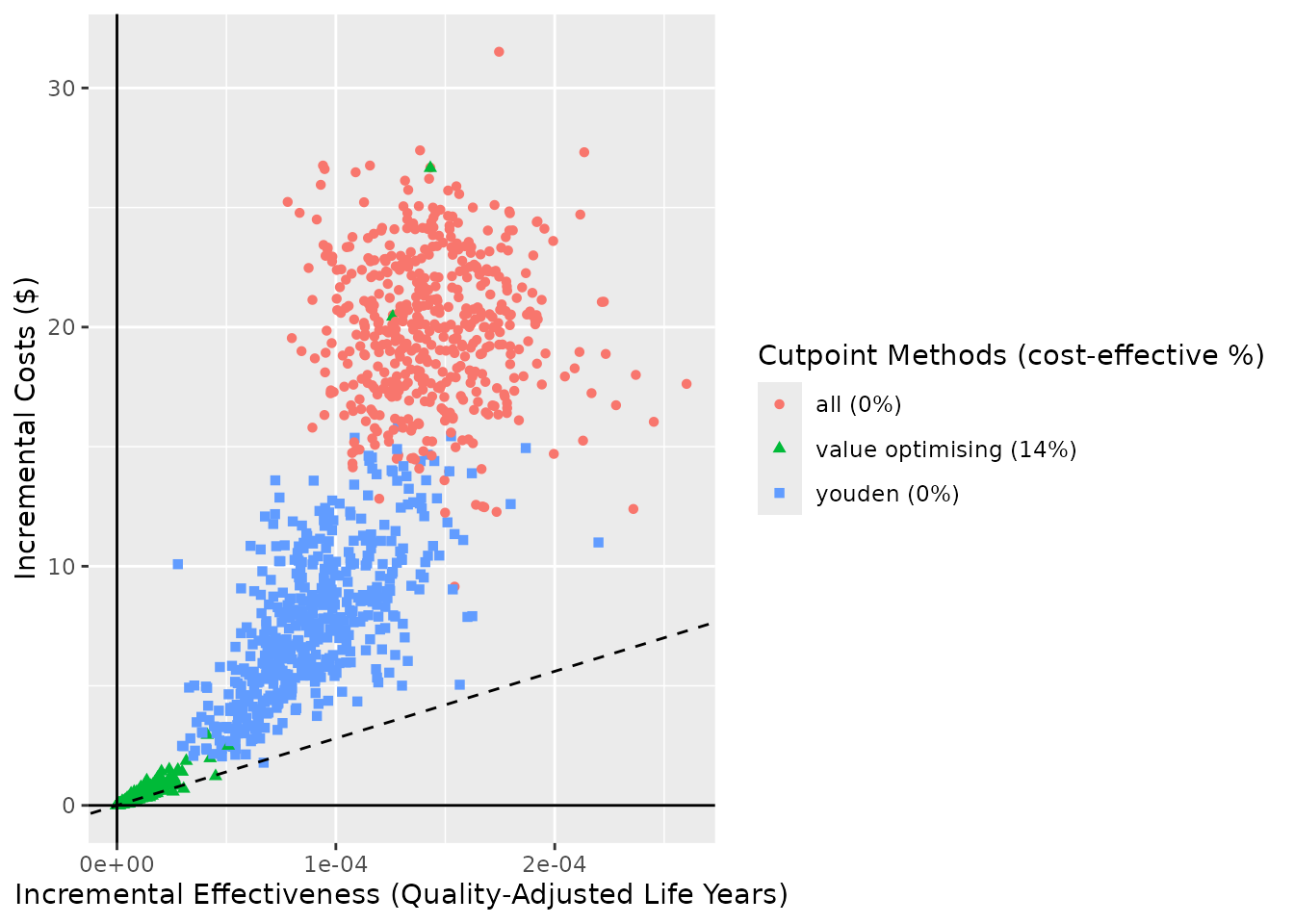

If you want the method to be mapped to shape but not colour, then, just as with any ggplot object, you can adjust the values on the returned plot with ggplot2::scale_color_manual().

ce_plot(do_nmb_sim_obj, ref_col = "none", shape = "method") + 
  ggplot2::scale_color_manual(values = rep("black", 3))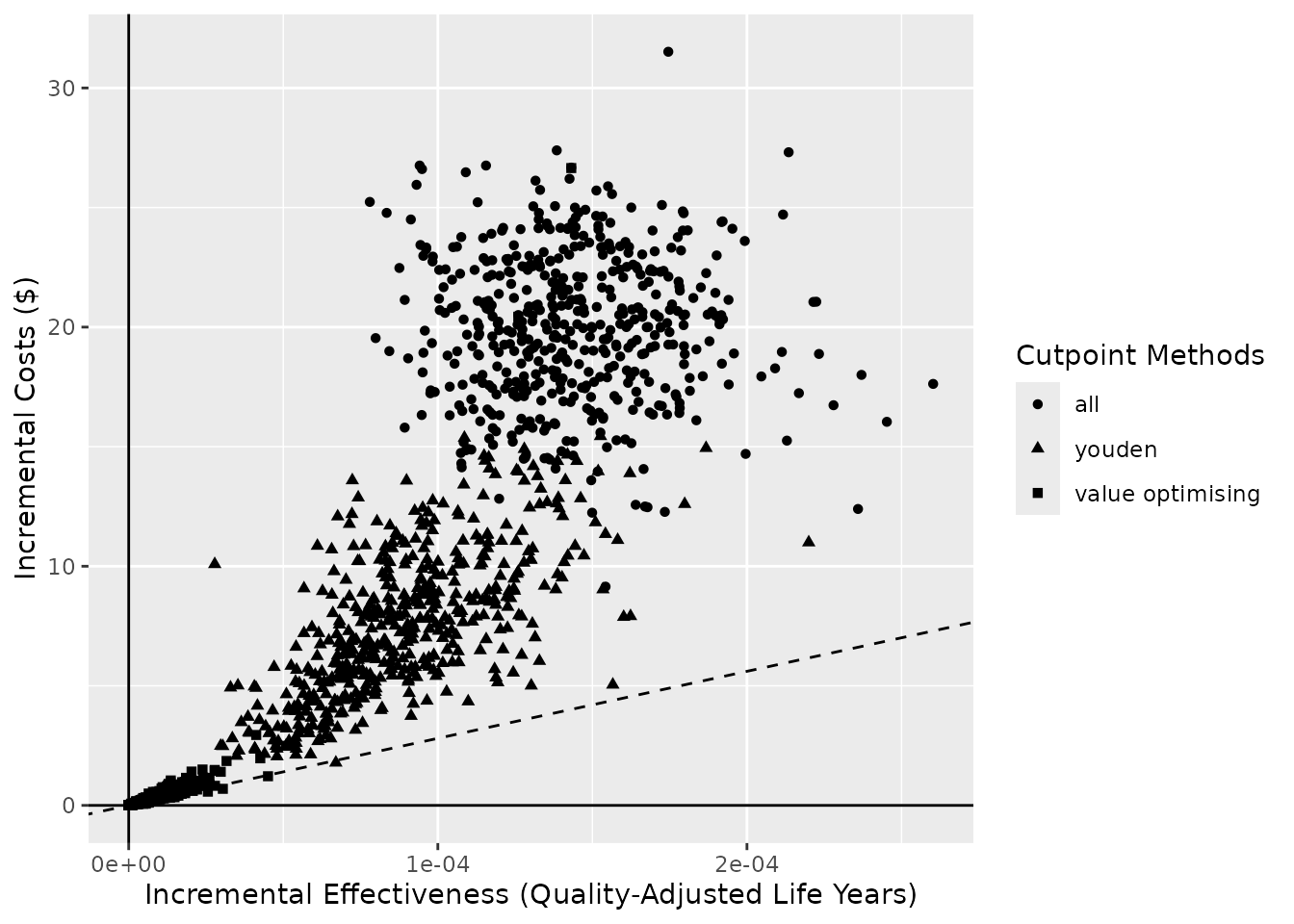

Making tables with predictNMB

To make tables from the same objects as we used for the plots, we instead use summary(). This can be applied to either type of object (screen_simulation_inputs() or do_nmb_sim()). Using the %>% (or |>) operator, we can pass it straight to flextable() from the flextable package that we have already loaded.

summary(sim_screen_obj)

sim_auc

event_rate

all_median

all_95% CI

none_median

none_95% CI

youden_median

youden_95% CI

value optimising_median

value optimising_95% CI

0.70

0.1

-26.07

-32.2 to -19.6

-10.02

-13 to -7.3

-14.94

-21.1 to -10.6

-10.10

-13.4 to -7.4

0.70

0.2

-31.68

-38.9 to -25.8

-20.26

-25.9 to -15

-22.95

-28.9 to -17.9

-20.27

-25.7 to -15.2

0.75

0.1

-26.19

-32.4 to -19.4

-10.05

-12.6 to -7.4

-13.90

-20.3 to -9.6

-10.15

-12.6 to -7.4

0.75

0.2

-32.17

-39.2 to -25.5

-20.35

-25.5 to -15.4

-22.74

-28 to -17.8

-20.16

-24.9 to -15.6

0.80

0.1

-25.84

-32.6 to -19.8

-10.17

-12.8 to -7.6

-13.22

-19 to -9.3

-10.15

-12.6 to -7.7

0.80

0.2

-31.89

-39.2 to -25.1

-19.97

-25.7 to -14.1

-21.49

-26.7 to -16.3

-19.58

-24.4 to -14.2

0.85

0.1

-26.11

-32.1 to -19.6

-10.06

-13.2 to -7.2

-12.30

-16.9 to -9.2

-9.97

-12.8 to -7.4

0.85

0.2

-31.77

-39.2 to -25.6

-20.02

-25.2 to -14.8

-20.70

-25.9 to -16.2

-19.34

-24.2 to -14.7

0.90

0.1

-26.10

-32.4 to -19.9

-10.07

-12.8 to -7.5

-11.43

-15.6 to -8.4

-9.73

-12.3 to -7.4

0.90

0.2

-32.19

-38.9 to -25.7

-20.25

-25.6 to -15.2

-19.84

-24.8 to -15.5

-18.78

-23.3 to -14.7

0.95

0.1

-26.09

-31.9 to -20

-10.11

-13.2 to -7.2

-10.29

-14.1 to -7.6

-9.27

-11.6 to -7.1

0.95

0.2

-32.13

-39.2 to -24.9

-19.70

-25.4 to -14.4

-18.35

-23 to -14.1

-17.76

-22.3 to -13.4

 
summary(do_nmb_sim_obj)

method

median

95% CI

all

-26.07

-32.2 to -19.6

none

-10.02

-13 to -7.3

value optimising

-10.10

-13.4 to -7.4

youden

-14.94

-21.1 to -10.6

By default, the methods are aggregated by the median and the 95% confidence intervals (and rounded to 2 and 1 decimal places, respectively). These are the default list of functions passed to the summary() as the agg_functions argument. These can be changed to any functions which aggregate a numeric vector.

summary(
  do_nmb_sim_obj,
  agg_functions = list(
    "mean" = function(x) round(mean(x), digits=2),
    "min" = min, 
    "max" = max
  )
)

method

mean

min

max

all

-26.04

-36.24787

-14.629660

none

-10.09

-14.82081

-6.340478

value optimising

-10.25

-32.57088

-6.390840

youden

-15.15

-23.81489

-9.037716

The what and rename_vector arguments work in the same way as they did when using autoplot().

summary(
  do_nmb_sim_obj,
  what = "inb",
  inb_ref_col = "all",
  rename_vector = c(
    "Value-Optimising" = "value_optimising",
    "Treat-None" = "none",
    "Youden Index" = "youden"
  )
)

method

median

95% CI

Treat-None

15.85

9.6 to 22

Value-Optimising

15.82

9.4 to 21.8

Youden Index

10.65

5.3 to 17.1

 
summary(sim_screen_obj)

sim_auc

event_rate

all_median

all_95% CI

none_median

none_95% CI

youden_median

youden_95% CI

value optimising_median

value optimising_95% CI

0.70

0.1

-26.07

-32.2 to -19.6

-10.02

-13 to -7.3

-14.94

-21.1 to -10.6

-10.10

-13.4 to -7.4

0.70

0.2

-31.68

-38.9 to -25.8

-20.26

-25.9 to -15

-22.95

-28.9 to -17.9

-20.27

-25.7 to -15.2

0.75

0.1

-26.19

-32.4 to -19.4

-10.05

-12.6 to -7.4

-13.90

-20.3 to -9.6

-10.15

-12.6 to -7.4

0.75

0.2

-32.17

-39.2 to -25.5

-20.35

-25.5 to -15.4

-22.74

-28 to -17.8

-20.16

-24.9 to -15.6

0.80

0.1

-25.84

-32.6 to -19.8

-10.17

-12.8 to -7.6

-13.22

-19 to -9.3

-10.15

-12.6 to -7.7

0.80

0.2

-31.89

-39.2 to -25.1

-19.97

-25.7 to -14.1

-21.49

-26.7 to -16.3

-19.58

-24.4 to -14.2

0.85

0.1

-26.11

-32.1 to -19.6

-10.06

-13.2 to -7.2

-12.30

-16.9 to -9.2

-9.97

-12.8 to -7.4

0.85

0.2

-31.77

-39.2 to -25.6

-20.02

-25.2 to -14.8

-20.70

-25.9 to -16.2

-19.34

-24.2 to -14.7

0.90

0.1

-26.10

-32.4 to -19.9

-10.07

-12.8 to -7.5

-11.43

-15.6 to -8.4

-9.73

-12.3 to -7.4

0.90

0.2

-32.19

-38.9 to -25.7

-20.25

-25.6 to -15.2

-19.84

-24.8 to -15.5

-18.78

-23.3 to -14.7

0.95

0.1

-26.09

-31.9 to -20

-10.11

-13.2 to -7.2

-10.29

-14.1 to -7.6

-9.27

-11.6 to -7.1

0.95

0.2

-32.13

-39.2 to -24.9

-19.70

-25.4 to -14.4

-18.35

-23 to -14.1

-17.76

-22.3 to -13.4

The summary table contains the same outputs for both do_nmb_sim() and screen_simulation_inputs(), but they are arranged slightly differently. Each row in table for this summary is for a unique set of inputs. By default, this is trimmed to include only those inputs that vary in our function call — here, sim_auc and event_rate — by using the show_full_inputs argument. By default, only the inputs that vary are shown. However, we can set show_full_inputs = TRUE to see more.

summary(sim_screen_obj, show_full_inputs = TRUE)

In the table below, we merge repeated values using merge_v() and add the theme_box() to make it a bit easier to read. (You can see more about making tables with flextable here.)

n_sims

n_valid

fx_nmb_training

fx_nmb_evaluation

sample_size

sim_auc

event_rate

min_events

meet_min_events

.sim_id

all_median

all_95% CI

none_median

none_95% CI

youden_median

youden_95% CI

value optimising_median

value optimising_95% CI

500

10,000

unnamed-nmb-function-1

unnamed-nmb-function-1

189

0.70

0.1

19

TRUE

1

-26.07

-32.2 to -19.6

-10.02

-13 to -7.3

-14.94

-21.1 to -10.6

-10.10

-13.4 to -7.4

246

0.2

49

2

-31.68

-38.9 to -25.8

-20.26

-25.9 to -15

-22.95

-28.9 to -17.9

-20.27

-25.7 to -15.2

139

0.75

0.1

14

3

-26.19

-32.4 to -19.4

-10.05

-12.6 to -7.4

-13.90

-20.3 to -9.6

-10.15

-12.6 to -7.4

246

0.2

49

4

-32.17

-39.2 to -25.5

-20.35

-25.5 to -15.4

-22.74

-28 to -17.8

-20.16

-24.9 to -15.6

139

0.80

0.1

14

5

-25.84

-32.6 to -19.8

-10.17

-12.8 to -7.6

-13.22

-19 to -9.3

-10.15

-12.6 to -7.7

246

0.2

49

6

-31.89

-39.2 to -25.1

-19.97

-25.7 to -14.1

-21.49

-26.7 to -16.3

-19.58

-24.4 to -14.2

139

0.85

0.1

14

7

-26.11

-32.1 to -19.6

-10.06

-13.2 to -7.2

-12.30

-16.9 to -9.2

-9.97

-12.8 to -7.4

246

0.2

49

8

-31.77

-39.2 to -25.6

-20.02

-25.2 to -14.8

-20.70

-25.9 to -16.2

-19.34

-24.2 to -14.7

139

0.90

0.1

14

9

-26.10

-32.4 to -19.9

-10.07

-12.8 to -7.5

-11.43

-15.6 to -8.4

-9.73

-12.3 to -7.4

246

0.2

49

10

-32.19

-38.9 to -25.7

-20.25

-25.6 to -15.2

-19.84

-24.8 to -15.5

-18.78

-23.3 to -14.7

139

0.95

0.1

14

11

-26.09

-31.9 to -20

-10.11

-13.2 to -7.2

-10.29

-14.1 to -7.6

-9.27

-11.6 to -7.1

246

0.2

49

12

-32.13

-39.2 to -24.9

-19.70

-25.4 to -14.4

-18.35

-23 to -14.1

-17.76

-22.3 to -13.4

References

Fenwick, Elisabeth, Deborah A Marshall, Adrian R Levy, and Graham Nichol. 2006. “Using and Interpreting Cost-Effectiveness Acceptability Curves: An Example Using Data from a Trial of Management Strategies for Atrial Fibrillation.” BMC Health Services Research 6 (1): 1–8.