Get started

Welcome to the slopes vignette, a type of long-form documentation/article that introduces the core functions and functionality of the slopes package.

Installation

You can install the released version of slopes from CRAN with:

install.packages("slopes")

Install the development version from GitHub with:

# install.packages("remotes")
remotes::install_github("ropensci/slopes")

Installation for DEM downloads

If you do not already have DEM data and want to make use of the package’s ability to download them using the ceramic package, install the package with suggested dependencies, as follows:

# install.packages("remotes")
remotes::install_github("ropensci/slopes", dependencies = "Suggests")

Furthermore, you will need to add a MapBox API key to be able to get DEM datasets, by signing up and registering for a key at https://account.mapbox.com/access-tokens/ and then following these steps:

usethis::edit_r_environ()
# Then add the following line to the file that opens:
# MAPBOX_API_KEY=xxxxx # replace XXX with your api key

Functions

Elevation

• elevation_add() Take a linestring and add a third dimension (z) to its coordinates
• elevation_get() Get elevation data from hosted maptile services (returns a raster)
• elevation_extract() Extract elevations from coordinates

Slope calculation

• slope_vector() Calculate the gradient of line segments from distance and elevation vectors
• slope_distance() Calculate the slopes associated with consecutive distances and elevations
• slope_distance_mean() Calculate the mean average slopes associated with consecutive distances and elevations
• slope_distance_weighted() Calculate the slopes associated with consecutive distances and elevations, weighted by distance
• slope_matrix() Calculate the slope of lines based on a DEM matrix
• slope_matrix_mean() Calculate the mean slope of lines based on a DEM matrix
• slope_matrix_weighted() Calculate the weighted mean slope of lines based on a DEM matrix
• slope_raster() Calculate the slope of lines based on a raster DEM
• slope_xyz() Calculate the slope of lines based on XYZ coordinates

Plotting

• plot_slope() Plot slope data for a 3d linestring

Helper functions

• sequential_dist() Calculate cumulative distances along a linestring
• z_value() Extract Z coordinates from an sfc object
• z_start() Get the starting Z coordinate
• z_end() Get the ending Z coordinate
• z_mean() Calculate the mean Z coordinate
• z_max() Get the maximum Z coordinate
• z_min() Get the minimum Z coordinate
• z_elevation_change_start_end() Calculate the elevation change from start to end
• z_direction() Determine the direction of slope (uphill/downhill)
• z_cumulative_difference() Calculate the cumulative elevation difference

Examples

This section shows some basic examples of how to use the slopes package.

First, load the necessary packages and data:

library(slopes)
library(sf)
#> Linking to GEOS 3.12.1, GDAL 3.8.4, PROJ 9.4.0; sf_use_s2() is TRUE
library(raster)
#> Loading required package: sp

# Load example data
data(lisbon_route)
data(dem_lisbon_raster)

Add elevation to a linestring

If you have a 2D linestring and a DEM, you can add elevation data to the linestring using elevation_add():

sf_linestring_xyz_local = elevation_add(lisbon_route, dem = dem_lisbon_raster)
head(sf::st_coordinates(sf_linestring_xyz_local))
#>              X         Y        Z L1
#> [1,] -88202.31 -105757.6 55.91552  1
#> [2,] -88201.67 -105762.3 55.52176  1
#> [3,] -88200.54 -105770.5 54.62495  1
#> [4,] -88199.42 -105778.7 50.82914  1
#> [5,] -88198.29 -105786.9 50.76749  1
#> [6,] -88205.89 -105786.3 49.22162  1

If you don’t have a local DEM, elevation_add() can download elevation data (this requires a MapBox API key and the ceramic package):

# Requires a MapBox API key and the ceramic package
# sf_linestring_xyz_mapbox = elevation_add(lisbon_route)
# head(sf::st_coordinates(sf_linestring_xyz_mapbox))

Calculate slope

Once you have a 3D linestring (with XYZ coordinates), you can calculate its average slope using slope_xyz():

slope = slope_xyz(sf_linestring_xyz_local)
slope
#>          1 
#> 0.07817098

Plot elevation profile

You can visualize the elevation profile of a 3D linestring using plot_slope():

plot_slope(sf_linestring_xyz_local)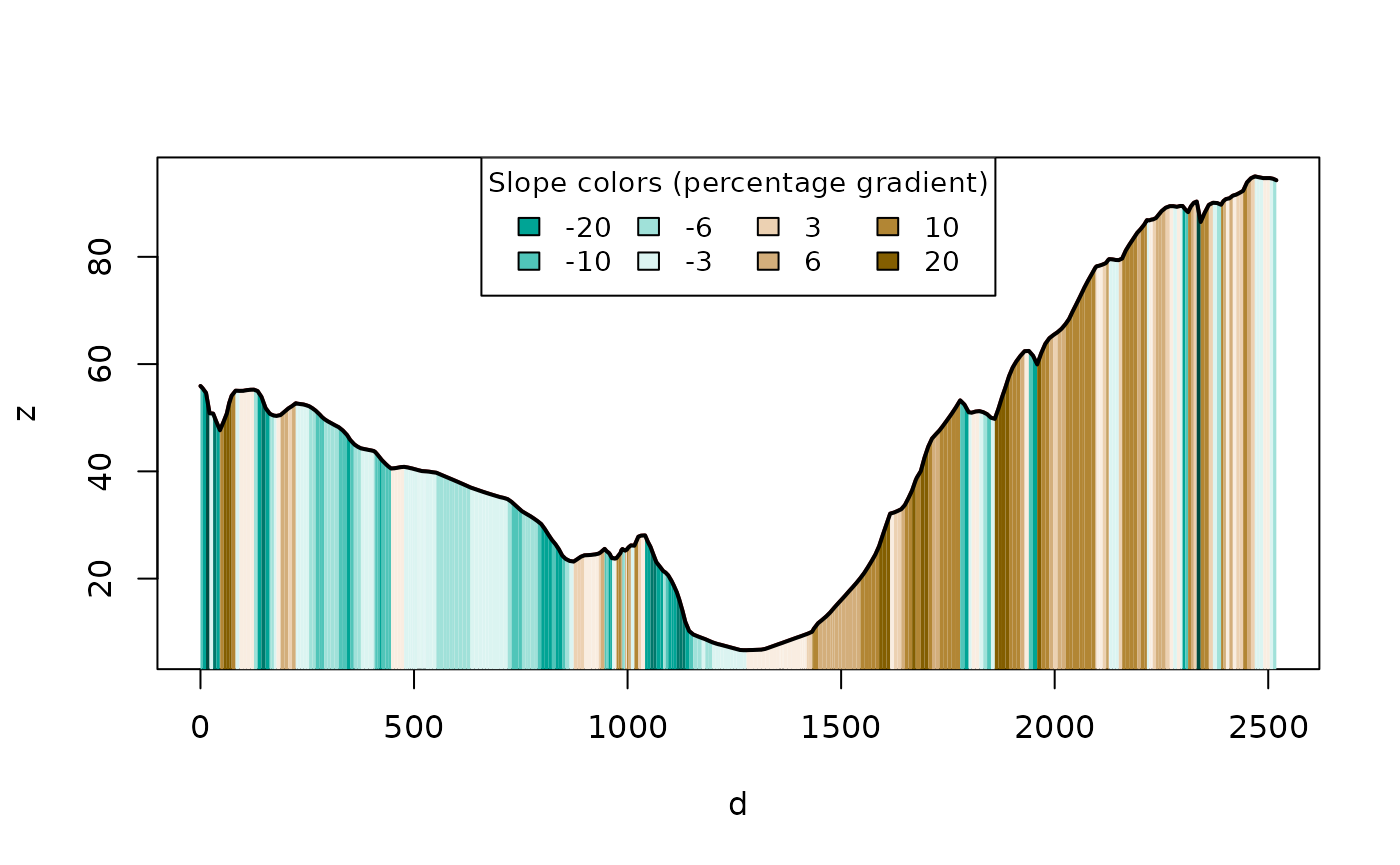

Working with segments

The slopes package can also work with individual segments of a linestring. First, let’s segment the lisbon_route:

lisbon_route_segments = sf::st_segmentize(lisbon_route, dfMaxLength = 100) # Arbitrary length
lisbon_route_segments = sf::st_cast(lisbon_route_segments, "LINESTRING")
# Add elevation to segments
lisbon_route_segments_xyz = elevation_add(lisbon_route_segments, dem = dem_lisbon_raster)

Now calculate the slope for each segment:

lisbon_route_segments_xyz$slope = slope_xyz(lisbon_route_segments_xyz)
summary(lisbon_route_segments_xyz$slope)
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#> 0.07817 0.07817 0.07817 0.07817 0.07817 0.07817

You can plot these segments, for example, colored by their slope. Here we use tmap for a more advanced plot (requires tmap package).

# Requires tmap package
# library(tmap)
# qtm(lisbon_route_segments_xyz, lines.col = "slope", lines.lwd = 3)

Alternatively, using base R graphics:

plot(st_geometry(lisbon_route_segments_xyz), col = heat.colors(length(lisbon_route_segments_xyz$slope))[rank(lisbon_route_segments_xyz$slope)], lwd = 3)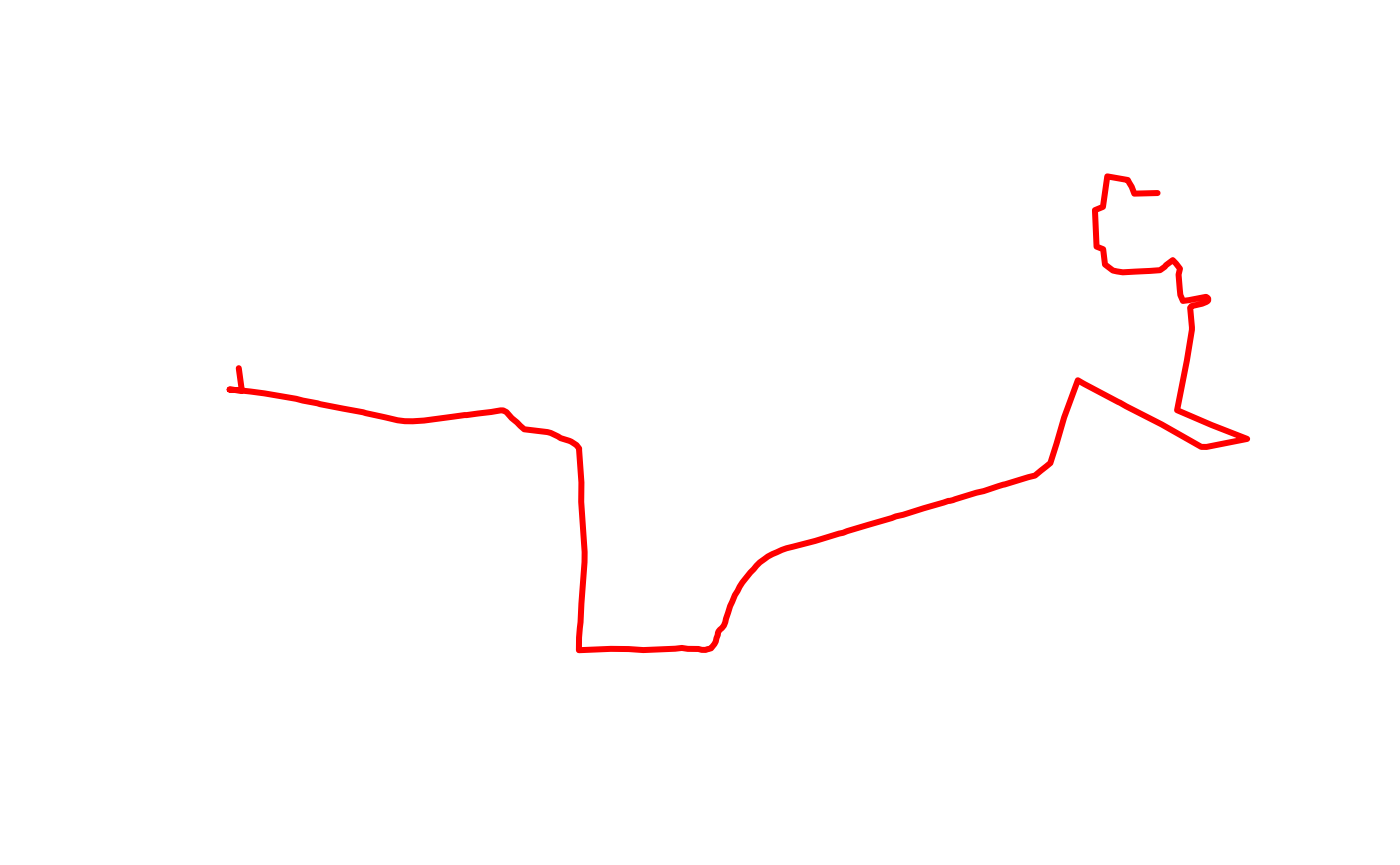

This vignette provides a basic overview. For more detailed information and advanced use cases, please refer to the other vignettes and the function documentation.