For bivariate data that show monotonic decreases (e.g. plots of trajectory count vs. frame gap allowed, or scree plots from PCAs), this function will find the "elbow" point. This is done by drawing an (imaginary) line between the first observation and the final observation. Then, the distance between that line and each observation is calculated. The "elbow" of the curve is the observation that maximizes this distance.
Arguments
- data_frame
A two-column data frame (numeric entries only), ordered x-axis first, y-axis second.
- export_type
If "row_num" (the default), the row number of the elbow point is returned. If anything else, the entire row of the original data frame is returned.
- plot_curve
Default FALSE; should the curve be plotted?
Value
If export_type is row_num the row number of the elbow
point is returned. If anything else is used for that argument, the entire
row of the original data frame on which the "elbow" is located is returned.
If plot_curve is TRUE, the curve is plotted along with a
vertical line drawn at the computed elbow point.
See also
Other mathematical functions:
calc_min_dist_v(),
deg_2_rad(),
get_2d_angle(),
get_3d_angle(),
get_3d_cross_prod(),
get_dist_point_line(),
get_traj_velocities(),
get_velocity(),
rad_2_deg()
Examples
df <- data.frame(x = seq(1:10),
y = 1/seq(1:10))
plot(df)
find_curve_elbow(df, plot_curve = TRUE)
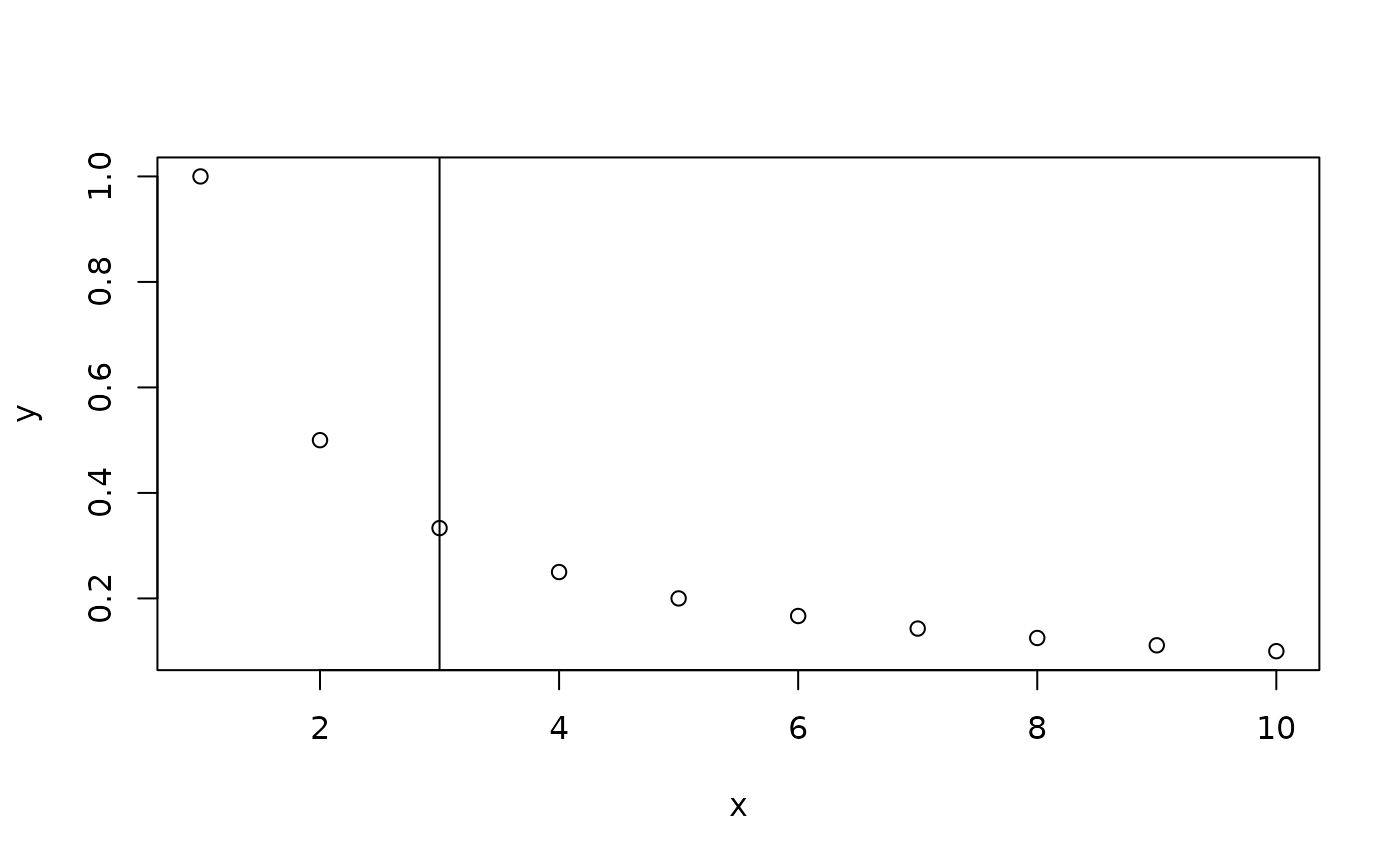#> [1] 3