Skip to contents

Convert series of overlapping lines into a route network

Source: R/overline.R
overline.Rd

This function takes a series of overlapping lines and converts them into a single route network.

This function is intended as a replacement for overline() and is significantly faster especially on large datasets. However, it also uses more memory.

Usage

overline(
  sl,
  attrib,
  ncores = 1,
  simplify = TRUE,
  regionalise = 1e+09,
  quiet = ifelse(nrow(sl) < 1000, TRUE, FALSE),
  fun = sum
)

overline2(
  sl,
  attrib,
  ncores = 1,
  simplify = TRUE,
  regionalise = 1e+07,
  quiet = ifelse(nrow(sl) < 1000, TRUE, FALSE),
  fun = sum
)

Arguments

sl

A spatial object representing routes on a transport network

attrib

character, column names in sl to be aggregated

ncores

integer, how many cores to use in parallel processing, default = 1

simplify

logical, if TRUE group final segments back into lines, default = TRUE

regionalise

integer, during simplification regonalisation is used if the number of segments exceeds this value

quiet

Should the the function omit messages? NULL by default, which means the output will only be shown if sl has more than 1000 rows.

fun

Named list of functions to summaries the attributes by? sum is the default. list(sum = sum, average = mean) will summarise all attributes by sum and mean.

Value

An sf object representing a route network

Details

The function can be used to estimate the amount of transport 'flow' at the route segment level based on input datasets from routing services, for example linestring geometries created with the route() function.

The overline() function breaks each line into many straight segments and then looks for duplicated segments. Attributes are summed for all duplicated segments, and if simplify is TRUE the segments with identical attributes are recombined into linestrings.

The following arguments only apply to the sf implementation of overline():

  • ncores, the number of cores to use in parallel processing

  • simplify, should the final segments be converted back into longer lines? The default setting is TRUE. simplify = FALSE results in straight line segments consisting of only 2 vertices (the start and end point), resulting in a data frame with many more rows than the simplified results (see examples).

  • regionalise the threshold number of rows above which regionalisation is used (see details).

For sf objects Regionalisation breaks the dataset into a 10 x 10 grid and then performed the simplification across each grid. This significantly reduces computation time for large datasets, but slightly increases the final file size. For smaller datasets it increases computation time slightly but reduces memory usage and so may also be useful.

A known limitation of this method is that overlapping segments of different lengths are not aggregated. This can occur when lines stop halfway down a road. Typically these errors are small, but some artefacts may remain within the resulting data.

For very large datasets nrow(x) > 1000000, memory usage can be significant. In these cases is is possible to overline subsets of the dataset, rbind the results together, and then overline again, to produce a final result.

Multicore support is only enabled for the regionalised simplification stage as it does not help with other stages.

References

Morgan M and Lovelace R (2020). Travel flow aggregation: Nationally scalable methods for interactive and online visualisation of transport behaviour at the road network level. Environment and Planning B: Urban Analytics and City Science. July 2020. doi:10.1177/2399808320942779 .

Rowlingson, B (2015). Overlaying lines and aggregating their values for overlapping segments. Reproducible question from https://gis.stackexchange.com. See https://gis.stackexchange.com/questions/139681/.

See also

Other rnet: gsection(), islines(), rnet_breakup_vertices(), rnet_group()

Other rnet: gsection(), islines(), rnet_breakup_vertices(), rnet_group()

Author

Barry Rowlingson

Malcolm Morgan

Examples

sl <- routes_fast_sf[2:4, ]
sl$All <- flowlines_sf$All[2:4]
rnet <- overline(sl = sl, attrib = "All")
nrow(sl)
#> [1] 3
nrow(rnet)
#> [1] 4
plot(rnet)

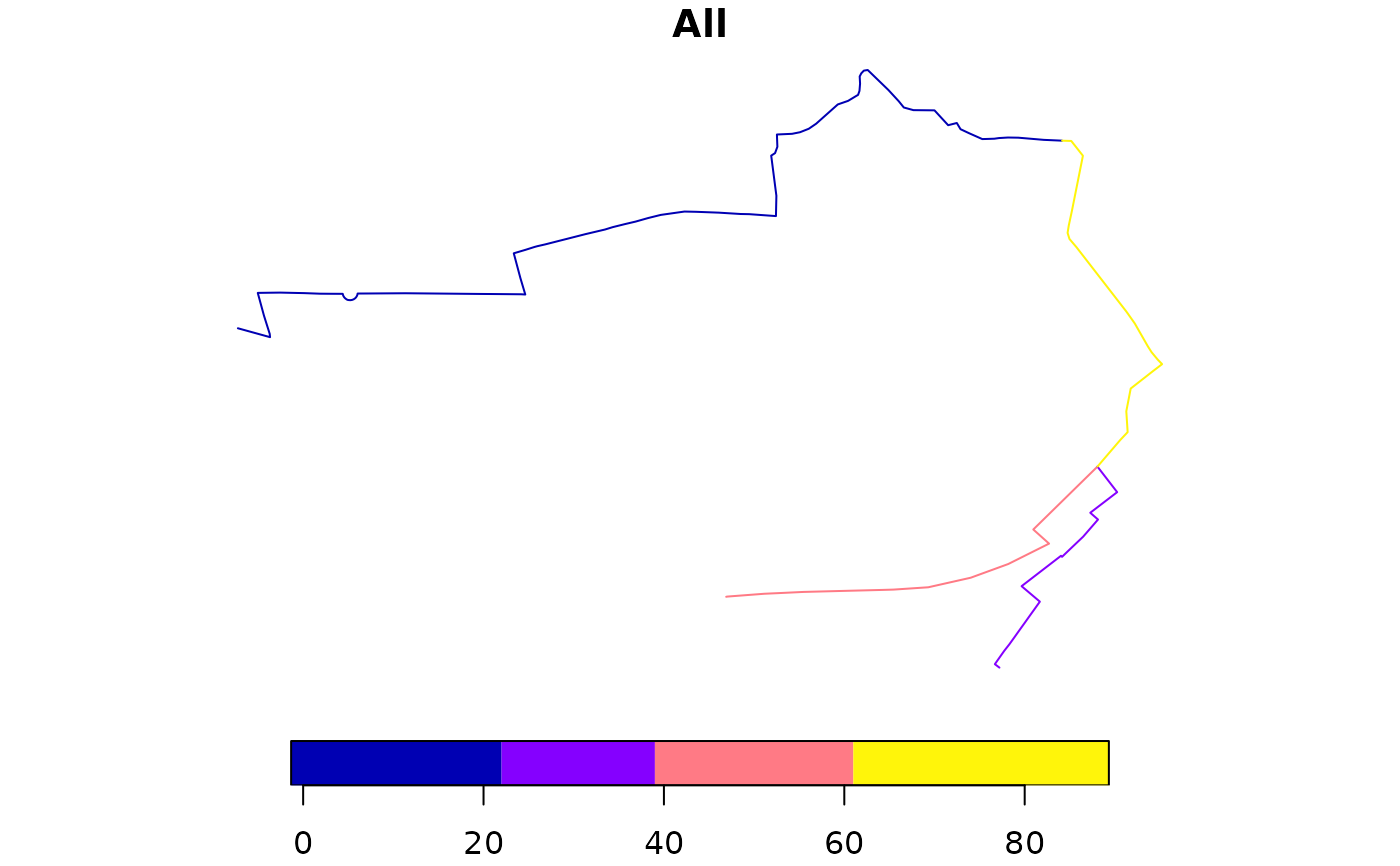rnet_mean <- overline(sl, c("All", "av_incline"), fun = list(mean = mean, sum = sum))
plot(rnet_mean, lwd = rnet_mean$All_sum / mean(rnet_mean$All_sum))

rnet_sf_raw <- overline(sl, attrib = "length", simplify = FALSE)
nrow(rnet_sf_raw)
#> [1] 151
summary(n_vertices(rnet_sf_raw))
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>       2       2       2       2       2       2 
plot(rnet_sf_raw)

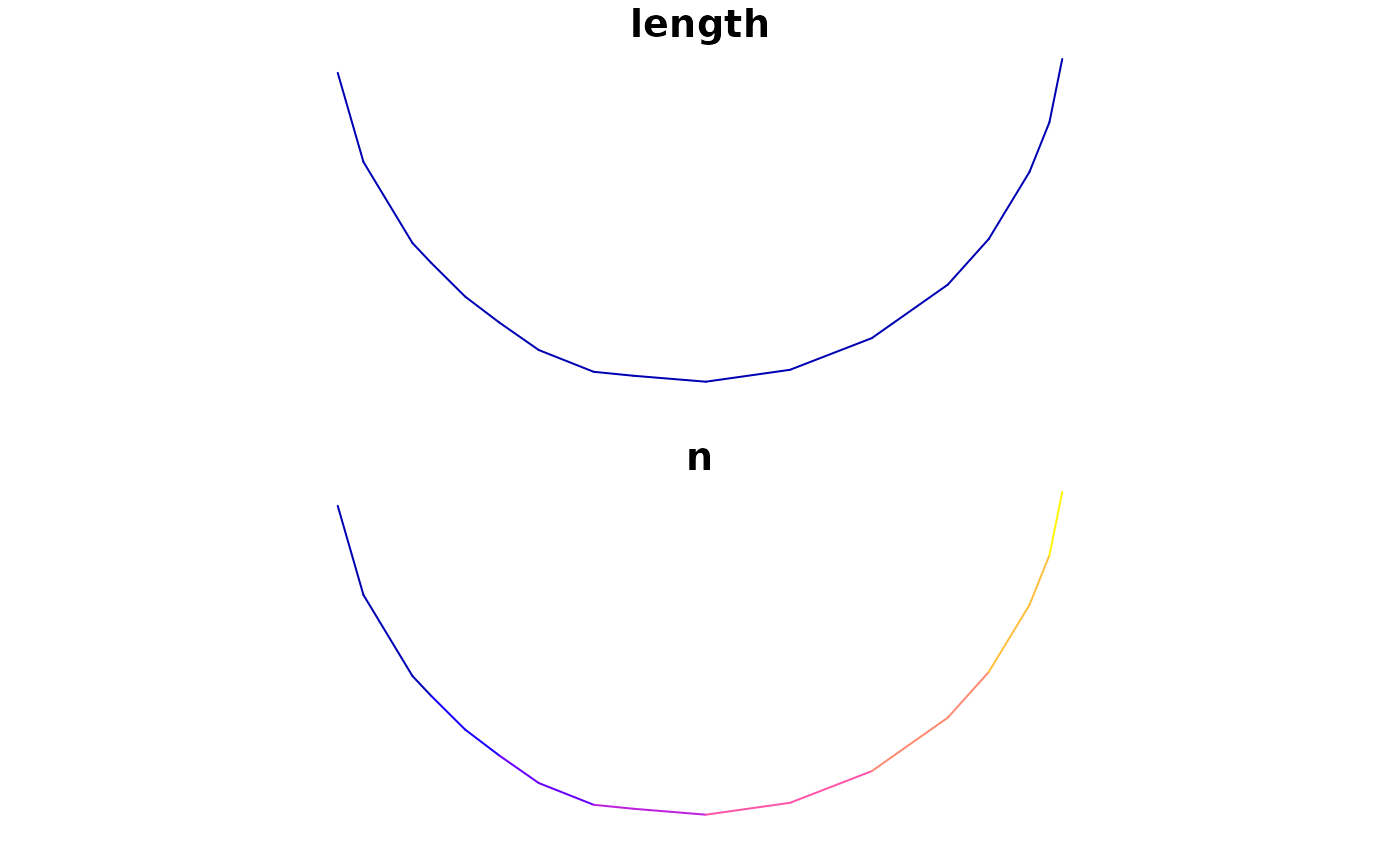
rnet_sf_raw$n <- 1:nrow(rnet_sf_raw)
plot(rnet_sf_raw[10:25, ])